The problem it solves Link to heading
Imagine you have an irregullary sampled time series, where at various time points we perform interventions. These interventions may influence the dynamics of the timeseries. The question we want to answer is:
If I perform a hypothetical sequence of interventions how will my time series evolve?
An example and some details Link to heading
Example Link to heading
As a medical doctor in a hospital, if a patient has a high fever and is at risk of dying, a common practice is to measure their levels of C-reactive protein (CRP) to determine if they need antibiotics. If the CRP level is high, antibiotics are administered at a certain dosage. However, the effects of antibiotics may not be immediate and it may take some time before they show. In this scenario, the doctor would wait for some time and measure the patient’s CRP levels again.
There are generally 3 outcomes that can occur in this scenario:
The CRP level decreases after antibiotics are administered, indicating that the infection is being successfully treated.
The CRP level remains unchanged or only slightly decreases, indicating that the antibiotics may not be effective for this particular infection or the dosage may not be sufficient.
The CRP level increases, indicating that the infection may be getting worse and a different course of treatment may be needed.
It is our decision to stick with the current treatment or change it.
Details Link to heading
We can visuallize the example above as:
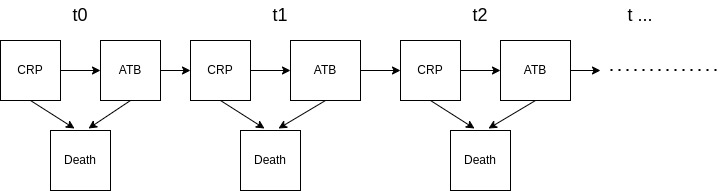
At every time step we measure the CRP levels of a patient. The CRP levels not only influence the dosage and type of antibiotics prescribed, but they also serve as an indicator of the patient’s likelihood of dying. Antibiotics are intended to lower the probability of death by reducing future CRP levels. This logic is intuitive, but there is a hidden catch: we have introduced time-dependent confounding. To understand this, let’s start by defining time-dependent variables and time-dependent treatment.
Time-Dependent variables Link to heading
Are variables that change over time and they are repeatedly measured. In our case CRP levels are a time-dependent variable
Time-Dependent treatment Link to heading
Treatment (or just action) that is a response to a change in time-dependent variable. In our case this the type and dose of antibiotics.
Time-Dependent confounding Link to heading
It is a confounder that is affected by the previous treatment. In our case the current dose (type) of antibiotics has an influence on future doses (types) of antibiotics. For those who have an machine learning background we can say that each treatment introduces an distribution shift.
Counterfactuals, confounding and bias Link to heading
At the beggining we asked the following question:
If I perform a hypothetical sequence of interventions how will my time series evolve?
We already introduced time-dependent confounding, so we know that each time we perform some sort of intervention it potentially can shift the distribution. In order to accurately determine the effect of a hypothetical sequence of interventions, it is crucial to take into account all past interventions and consider how each new intervention could potentially affect the distribution further.
If we want to have an unbiased counterfactual estimate we have to remove confounding (close all the back doors).
Treatment Effect Neural Controlled Differential Equation (TC-CDE) Model Link to heading
The main idea is to use time-dependent variables and treatments to fit a neural controlled differential equation (NCDE). An NCDE is a type of differential equation where the vector field is represented by a neural network. The solution to the equation is not only determined by its initial conditions, but also by subsequent observations.
For example, in the context of inflammation, we can view inflammation as a latent process that evolves over time due to the immune system or medication. CRP levels are realizations of this latent process. Modeling this process can be difficult, but the TC-CDE model addresses this by expressing the latent process as a solution to an NCDE.
However, for counterfactual estimation, modeling the latent process as an NCDE is not sufficient. To achieve an unbiased counterfactual estimate, we need to ensure that the latent process is not predictive of the treatment that will be administered. Additionally, we need to ensure that administering a treatment at time t will not change the latent value at time t, but only influence its future latent dynamics.
A bit of Math Link to heading
I always try to avoid using equations, but I don’t always succeed. For those who are more familiar with machine learning and haven’t seen differential equations in a while (or ever), the strange integral can be viewed as the temporal evolution of some state. The dynamics of the evolution are governed by a differential equation.
Latent Path Link to heading
To get the latent path we first have to define the initial state:
$$Z_{t0} = g_{\eta}(X_{t0},A_{t0}, Y_{t0})$$
- $g_{\theta}$ is a neural network that takes the initial covariates $X_{t0}$, treatment assignment $A_{t0}$ and observed outcome $T_{t0}$ and produces the initial latent space embedding $Z_{t0}$
Next we define our evolution of the initial state:
$$Z_t = S_{t0} + \int_{t_0}^t f_{\theta}(Z_s) \frac{d[S_s, A_s, Y_s]}{ds}ds $$
for $t \in (t_0, t]$
- $Z$ is a response that is a solution to NCDE
- $f_{\theta}$ is the latent vector field parametrized by a neural network
Objective function Link to heading
To mitigate confounding bias we have to make sure that the latent path is not predictive of future treatments to achieve this we introduce 2 neural networks:
$h_v: R^l \rightarrow R^d$ used to predict the outcome $\hat{y}_s = h_v(Z_s)$
$h_a: R^l \rightarrow [0,1]$ used to predict the treatment $\hat{p}s = \hat{p}(a_s = 1) = h{a}(Z_s)$
If there are k>1 observations in the timewindow $[t,t’]$ with observation times $(t_1, \cdots, t_k)$ our loss function is defined as
$$L = \frac{1}{n}\sum_{i=1}^n L_i^{(y)} - \mu L_i^{(a)} $$
- $L^{(y)} = \frac{1}{k} (y_{t_j} - \hat{y}_{t_j})^2$ this is the sequare mean of outcome prediction
- $L^{(a)} = - \frac{1}{k} \sum_{j=1}^k a_{t_j} \log(\hat{p}{t_j}) + (1-a_j)\log (1 - \hat{p}{t_j})$ this is the cross entropy of treatment predictions
Since there is a substraction before $\mu$ we essentially maximize the cross entropy ensuring that $z_t$ is not predictive of the treatment assignment $A_t$. This leads to balancing representations removing bias form time-dependent confounders allowing reliable counterfactual estimation where $\mu$ controlls the tradeoff between treatment and outcome predictions.
Hypothetical path Link to heading
Our initial goal was to evaluate the effect of some hypothetical treatment schedule. Because of this we need to go from $t$ to some future $t’$:
$$Z_{t’} = Z_t = \int_{t}^{t’}f_{\theta}(Z_s)\frac{dA_s}{ds}ds $$
- $Z_t$ is the encoded latent state of a patient up to time t
- $A_s$ is the hypothetical treatment schedule $t < s < t'$
To get the predicted outcome we use our neural network trained before
$$\hat{y}{t’} = h_v(Z{t’})$$
Summary Link to heading
Being able to generate unbiased estimates of some outcome value given hypothetical treatment schedules (or just some sort of actions) is a powerful tool. And not requiring an fixed schedule for these actions makes it also very versatile. And I look forward for extensions on these method.
Disclaimer Link to heading
I did read the original paper, and look at the code that was supplied with it. I did write this article on my own, however since I am not a native speaker, I did use ChatGPT for proof reading and improving my writing. If you are really interested how the original was worded. I will provide a link below.