Abstract Link to heading

It is notoriously expensive to train a Language Model from scratch, making independent research impossible and trying out new architectures extremely risky. Because of these costs, Transformer++ models like LLaMa, based on Rotary Embedding, SwiGLU, MLP, RMSNorm, without linear bias, sometimes with grouped query attention and/or sliding window attention, are the de facto standard, not because they are the best, but because they are proven to work! In previous posts I covered SSM-Transformer Hybrids. The biggest benefit of hybridization is their reduced inference cost and minimal memory overhead due to reduced KV cache, and combining SSMs can Attention can make the model more expressive. The biggest obstacle of these models is that they need to be pretrained from scratch. For example Zamba2 7B, is a 7B model that was trained on 128 H100 GPUs for 50 days, bringing its pretraining costs to around 600K US dollars. This makes it one of the cheapest (but by far not weakest) SSM-Attention hybrids, however if we look into detail the model was trained only on 3T (+100B high quality for annealing) tokens. In comparison Llama3 was trained on 15T tokens, if we would apply the same number of tokens to Zamba we would end up with costs around 3M US dollars. It is not hard to see that these kinds of budgets are out of scope for any individual, but also out of scope for many medium sized research organizations and academia.

In this post we look into the details of two distillation techniques that take an already pretrained Transformer model and replace some of its parts with a Mamba-like State Space model. The biggest benefit of this approach is that we can drastically decrease the inference costs while avoiding the whole pretraining procedure on trillions of tokens, and still maintain the same performance level by finetuning on a few billion tokens.

• (Mohawk) Transformers to SSMs: Distilling Quadratic Knowledge to Subquadratic Models
• Mamba in the Llama

Sequence and Channel mixers! Link to heading

Let’s revisit some key concepts of Transformers and Self attention. So what is self-attention? Remember, for a causal model, every output token is just a weighted sum of the input tokens. Yes you can have more heads, but that will just give you multiple weighted sums, preferably somewhat different (each head should capture different variation in the data). If you read, which I hope you did, my post about Monarch Matrices, there I did a breakdown of an Attention Block into two parts: first part is the Sequence Mixer, and the second the Channel Mixer. Self-Attention is a Sequence Mixer - it may not be the most efficient in terms of computation, being quadratic in computation and needing a KV cache so we do not recompute the token representations over and over each time we sample a new token. The MLP parts of an Attention block serve as Channel Mixers. MLP also plays another crucial role, since it is theorized that it holds most of the LLMs knowledge!

Matrix Orientation, Hidden-State Alignment, Weight-Transfer and Knowledge Distillation (Mohawk) Link to heading

The goal of Mohawk is to take a Transformer model (in our context this is a Teacher Model), and replace some (or all) self-attention parts with Mamba2 (this we will call Student Model). The knowledge transfer happens in 3 stages, where in each consecutive stage we train more parameters, each responsible for transferring different information.

Stage 1 Link to heading

In the first stage, we focus on aligning the Sequence Mixers between the Student Model and the Teacher model. For example, if we were to distill from Llama3, we would align the output from here.

Objective

$$\min_{\phi}||\text{TeacherMixer}(u) - \text{StudentMixer}_{\phi}(u) ||_F$$

• $u$ is the output of the preceding layer of the Teacher

Remark! Link to heading

This optimization can run in parallel, and we can precompute the Teacher part in advance. It is crucial that both teacher and student mixer have the same preceding transformations, which means they take input and produce outputs of the same shape.

Modifications to Mamba Link to heading

Mamba and Mamba2 are richer than the self-attention operation since they can also act as Channel Mixers. Because of this, the authors made one modification to Mamba, which is replacing the local convolution with the identity operation. This nullifies its effect, and according to the following research, it is not really needed since Mamba itself is expressive enough to capture this information.

Stage 2 Link to heading

As mentioned in stage 1, the role of self-attention in an attention block is to perform sequence mixing. In stage 2, we go a step further and align the whole Attention block.

Objective $$ \min_{\phi}||\text{AttentionBlock}(u) - \text{StudentMixtureBlock}_{\phi} (u)||_2$$

Here it is worth noting that Mamba(2) is also the channel Mixer, thus the student block essentially stays the same between stages 1 and 2. We can view Stage 2 as a correction to Stage 1, which by itself pushes the attention weights in a slightly wrong direction. As with Stage 1, we can train all the blocks in parallel, on materialized data.

Modifications to Mamba Link to heading

The authors decided to remove the Normalization layers, and they set the gate to 1 to cancel out its initial effect.

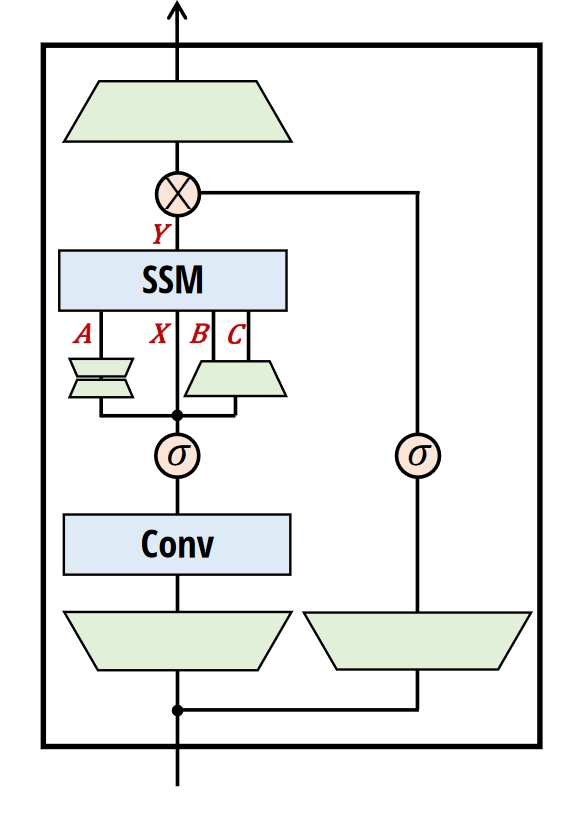
Stage 3 Link to heading

Here we are going to train the student model as a whole, but first we transfer the remaining parts from the teacher model. These remaining parts are:

• MLPs, which we will freeze since they should contain most of the model’s learned knowledge
• initial embedding layer
• final layer normalization
• language modeling heads
• input normalization of each block

Objective

$$ \min_{\phi}L_{CE}(\text{TeacherModel}(x), \text{StudentModel}_{\phi}(x)) $$

This is a very common approach where the student tries to mimic the distribution of the teacher.

Phi Mamba Link to heading

To showcase the effectiveness of this approach, the authors distilled two hybrid models. Since they used the stellar Phi-1.5 as the teacher model, they coined the models Phi-Mamba.

Architecture Link to heading

Phi-Mamba retains 4 attention layers, with the rest replaced by Mamba2. However, as mentioned above, there are some modifications to the original architecture:

• removed post convolution activation
• set convolution to identity, disabling this feature
• removed pre-output normalization
• changed from multi-value to multi-head to match the behavior of attention
• dropped the discretization by making A purely input dependent

These modifications are not too major and do not require changes to the SSD algorithm.

Results Link to heading

The actual training was done on 3 Billion tokens! Yes billions, not trillions! At the beginning of the post we saw that Zamba2 7B was pretrained on 3T tokens with an estimated budget of around 600k. By naively extrapolating, we could say that Mohawk enables distillation at 0.1% of the cost, making it around 600 US Dollars. Yes sure, there are vast differences in the architecture, but this is again one of the first steps in exploring new architectures with shortcuts in pretraining.

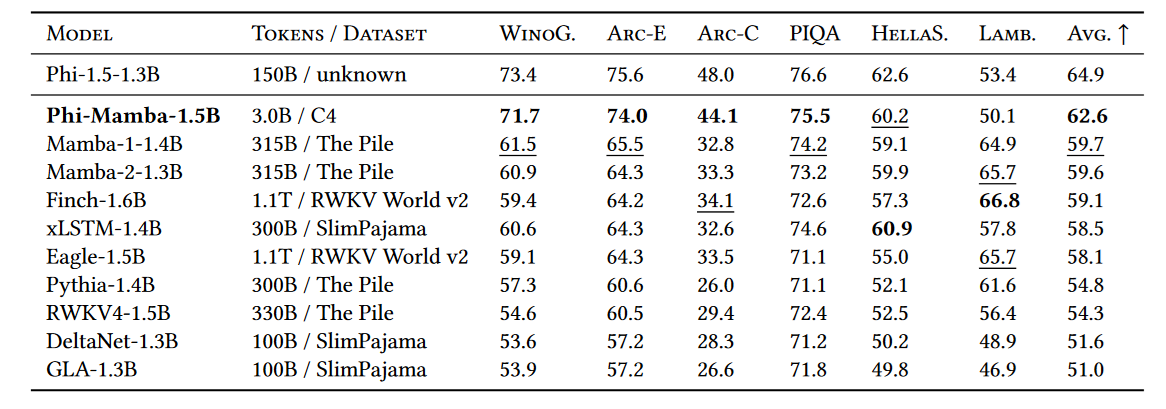
The actual token distribution was 80M for Stage 1, 160M for Stage 2, and 2.78B for Stage 3.

Stage Importance Link to heading

To better grasp the importance of various stages, the authors decided to train 3 models:

• Phi-Mamba is a pure Mamba2 model
• H-Phi-Mamba is the hybrid
• Phi is a pure transformer model, created by randomly reinitializing the student’s attention weights

All the models were distilled with Mohawk on 5B tokens instead of 3B.

We can see that most of the training budget was spent on Stage 3, and we spent relatively little in the first 2 stages. However, we can see massive gains. Even when we just apply stages 2 and 3, we get improvements compared to performing vanilla knowledge distillation. And lastly, even a bit of Stage 1 is key for the student to retain the teacher’s performance.

Remarks Link to heading

The idea of mixer-wise alignment for knowledge distillation is still in its infancy. However, it is an extremely cool concept, and it enables creating new models without the need for expensive pretraining. However, as we can see, there are still strict constraints on how a student model can look, where Mamba2 is used to mimic the behavior of self-attention.

Mamba in the Llama Link to heading

To a certain degree, the authors build upon the research done in [State Space Duality], which focused on the connection between Linear Attention and the Recurrent form of State Space Models.

From Linear Attention to a Linear RNN Link to heading

To recap, let’s start with standard masked multi-head Attention $$Q_t = W^Qo_t, K_t = W^Ko_t, V_t = W^Vo_t, \text{ for all t} $$ $$ \alpha_1, \cdots, \alpha_T = \text{softmax}([Q^T_qK_q, \cdots, Q^TK_T]/ \sqrt{D}) $$ $$ y_t = \sum_{s=1}^t m_{s,t}a_sV_s $$

• $m_{s,t} = 1(s \le t)$ is our causal mask

By dropping softmax, we can reexpress it as:

$$ y_t = \sum{s=1}^tm_{s,t}a_s V_s = \frac{1}{\sqrt{D}}Q_t \sum_{s=1}^t(m_{s,t}K_s^TV_s) = \frac{1}{\sqrt{D}} Q_t \sum_{s=1}^tm_{s,t}K_s^TW^vo_s $$

If we compare it to the definition of a Linear Recurrent Neural Network:

$$h_{t} = A_t h_{t-1} + B_t x_t $$ $$ y_t = C_t h_t $$

It’s not hard to see that there is a lot of similarity, and we can express linear Attention as a Linear RNN

$$h_t = m_{t-1,t}h_{t-1} + K_t V_t $$ $$ y_t = \frac{1}{\sqrt{D}}Q_th_t$$ $$ \downarrow $$

$$ h_t = A_t h_{t-1} + B_t x_t$$ $$ y_t = C_t h_t $$ $$ A_t = m_{t-1,t}, B_t = W^Ko_t, C_t = W^Qo_t, x_t = W^vo^t $$

However, there is a catch: $h \in R^{N \times 1}$, which means that the hidden state is capable of storing only one scalar over time per hidden dimension, greatly reducing its expressivity! This is one of the main reasons why linear attention did not become more mainstream. Luckily for us, Mamba (and Mamba2) provides an efficient way to expand the hidden state size while still maintaining the nice recurrent form.

Deriving Mamba from Attention Link to heading

First, let’s recap the Mamba equation:

$$h^t(k) = A_h(k) + B(k)x(k) $$ $$ y(k) = C(k)h(k) $$ Here A is a diagonal matrix and the rest is a continuous signal

We can now use V, K, Q from attention to initialize x, B, C of Mamba:

This introduces a couple of extra parameters. First, there is a need for a Neural Network to perform the discretization of the continuous signal, and second, we need the values for A. As it turns out, by reusing attention weights, we greatly jumpstart the model’s performance:

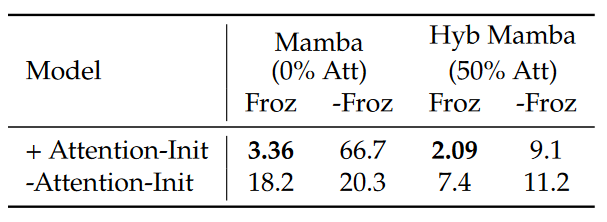
This figure compares two models: one is a pure Mamba model and the second is a 50% Hybrid. We compare the Perplexity of both models, and it’s clearly obvious that Attention initialization leads to significantly lower perplexity, which is most evident in a pure Mamba model!

Hybrid Model Link to heading

We already have an algorithm that is efficient at reusing attention weights, let’s see how far we can go and how many attention layers we can transfer.

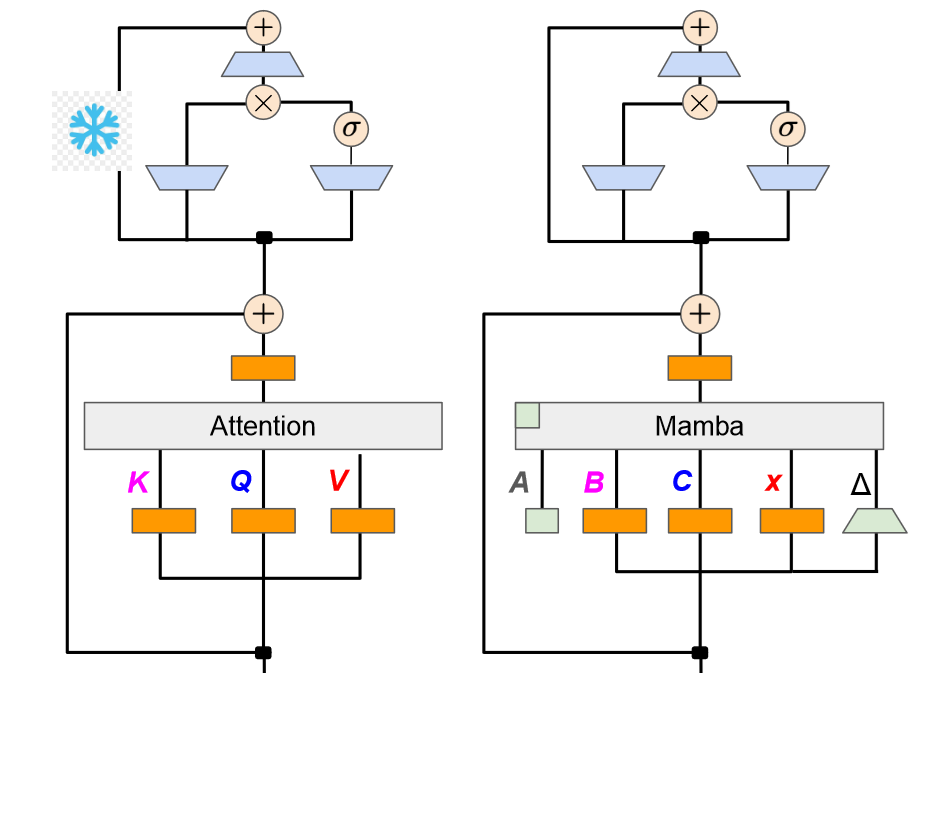
It is crucial to note that we freeze most of the remaining layers, especially the Fully Connected layers, since they should contain most of the model’s knowledge! We only train the transferred weights and the extra parameters.

Knowledge Distillation Link to heading

We can divide Mamba in the Llama’s knowledge distillation into two parts:

1. Supervised Fine-Tuning

Here we combine two approaches:

• Word level KL divergence, where the student is forced to match the whole probability distribution of the teacher over the entire set of tokens

$$ \text{KL}(p(.| \hat{y_{1:t}}, x, \theta_T) || p(.|\hat{y}_{1:t}, x ,\theta))$$

• Sentence Level Knowledge Distillation (SeqKD), where the student is optimized on the output of the teacher ($\hat{y}{1 \cdots t}$, also known as pseudo-labels) instead of the ground truth $y{1,\cdots, t}$.

$$\sum_{t=1}^T \alpha \log p(\hat{y_{t+1}}| \hat{y}_{1:t}, x, \theta)$$

The overall objective is just the weighted combination of both:

$$L(\theta) = - \sum_{t=1}^T \alpha \log p(\hat{y_{t+1}}| \hat{y}_{1:t}, x, \theta) + \beta $$

2. Preference Optimization By performing supervised finetuning in the first part, we undo the preference optimization performed on the original model. By reintroducing it, we should gain extra performance. The authors leveraged Direct Preference Optimization (DPO), where the teacher acted as the reference model.

Here is the objective:

$$ \max_{\theta}E_{x \sim D, y \sim p(y|x;\theta)}[r_{\phi}(x,y)] - \beta KL(p(y|x;\theta) || \theta(y| x; \theta_{\text{Teacher}}) $$

• $r_{\phi}(x,y)$ is a reward function, where $\phi$ is optimized with regard to the reward
• since we use DPO, we do not have a reward model as in reinforced learning, it is just classification since it is basically just supervised learning.

Data Link to heading

For the teacher’s pseudo labels we leverage: UltraChat and UltraFeedback, for the word level objective we use GenQua, InfinityInstruct and OpenHermes 2.5.

For DPO we use UltraFeedback if the teacher is Zephyr and SimPO and Zephyr if the teacher is Llama3.

Overall we train on 20B Tokens!

Experiments Link to heading

We use two teacher models: Zephyr-7B and Llama3-instruct. In student models, we replace attention by either Mamba or Mamba2 with 50%, 25%, 12.5% or 0% of retained attention layers.

Results Link to heading

For a chat Specific benchmark:

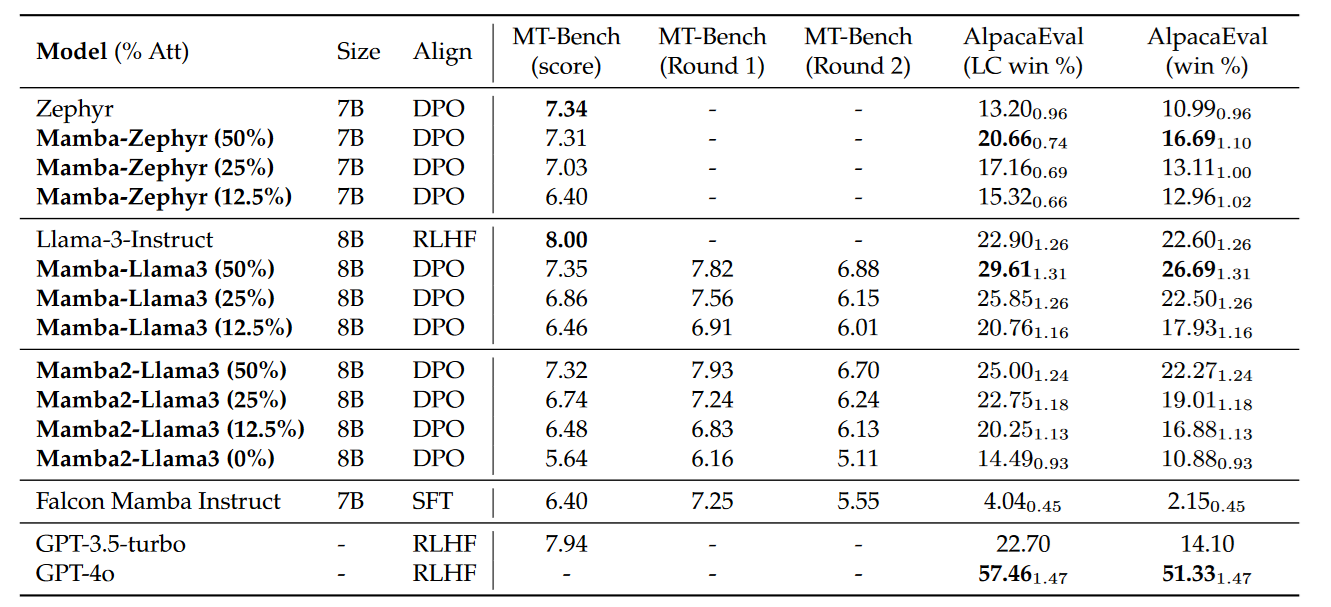
For a more general benchmark:

To a certain degree, the results are somewhat disappointing. It is clearly obvious that replacing Attention with Mamba hurts, especially in cases where we drop most of the attention layers.

Final Impression Link to heading

My first impression to both distillation methods were disappoint, especially if we look at the performance of hybrid models - the best performance was achieved in cases where we retained more attention layers. Before I thoroughly read the papers I had high hopes that it would be applicable to more experimental models, however in both cases the hybrid models were nearly a 1-to-1 match to their transformer counterparts. To a certain degree this makes sense, as most of the knowledge in Transformer models is kept in the channel mixer (FFN) part. Now Mamba can perform both sequence and channel mixing at the same time, which means that it is able to store a lot of knowledge! This is most obvious in models like Zyphra (2), where we have a lot of stacked Mamba blocks with minimal attention.

Still, this is one of the first papers that discusses cross-architecture knowledge distillation, and even with the shortcomings, the results are promising.