High level overview Link to heading
By combining State Space Models (SSMs) with Attention, we get a model that generates text more efficiently, with a speed increase of approximately 1.6 times. Additionally, this approach requires less paremters, enabling the development of larger models on existing hardware.
Language modeling requirements Link to heading
The Transformer architecture, which forms the basis of ChatGPT, is riding high on the hype train due to its impressive performance. Although it is just a basic Transformer, it has proven to be extremely effective. The reason for its success is explored in the paper “In-Context Learning and Induction Heads.” The authors argue that the majority of the in-context learning capacity of the Transformer architecture can be evaluated by two tests:
The Induction Head Task Test evaluates a model’s ability to recall context after encountering a special token. The test requires the model to recall the token that immediately followed the special token earlier in the sequence.
The Active Recall Task Test is similar to the Induction Head Task Test, but involves remembering multiple key-value pairs.
Attention, a key component of Transformers, has both Inductive Head and Active Recall capabilities. It compares tokens by constructing the quadratic attention matrix $QK^T$ and recalls tokens by applying the softmax function to the attention matrix and multiplying by $V$.
Therefore, a model that performs well on these two tests is likely to also perform well in language modeling.
State Space Models Link to heading
SSM is a type of Hidden Markov Model where the hidden state is continuous. Most people know SSMs trough Kalman Filtering, a well-known algorithm in the field of Bayesian filtering, is an exact method for solving Linear-Gaussian SSMs.
In the era of neural networks, SSMs can be expressed as the following layer:
$$y = SSM_{A,B,C,D}(u)$$
where $A,B,C,D$ are parameters learned using gradient-based optimization.
A closer examination of the layer would reveal:
$$x_i = Ax_{i-1} + Bu_i $$ $$y_i = Cx_i + Du_i $$
where $x$ represents the hidden state, $u$ is an input from the user, and $y$ is the output.
Benefits Link to heading
SSMs allow for efficient generation of sequences, as the next entry in the series only depends on the current state. This allows for extrapolation of larger sequences beyond those seen during training.
Downsides Link to heading
The recurrent nature of SSMs can lead to high IO overhead and inefficient hardware utilization, due to cache misses. To mitigate this issue, we can employ convolutions to improve performance.
Convolution and Fast Fourier Transform (FFT) Link to heading
For efficient traning we can write the entire sequence of input $u_1, \cdots, u_N$, the output sequence $y_1, \cdots, y_N$ as a confolution of the input with the filter f
$$f = [CA^0B, CAB, CA^2B, \cdots, CA^{N-1}B]$$
Given an initial condition $x_0$ we get
$$y_i = CA^iBx_0 + (f*u)_i + Du_i$$
- $(f*u)$ is the linear convolution
More generally any linear time-invariant system (SSM is a special case) can be expressed as a convolution.
Fast Fourier Transform (FFT) Link to heading
Convolution is still pretty expensive $O(N^2)$ however we can speed it up using FFT.
$$(f * u) = iFFT(FFT(f) \odot FFT(u))$$
Esentially we take the FFT of booth f, and u, multiply and take the inverse the FFT. This brings down the computational costs to $O(N \log N)$.
H3 layer Link to heading
The Hybrid SSM+Attention architecture aims to combine the strengths of both SSM and Attention to handle tasks that require both capturing context and efficient computation. By projecting the input $u$ into $Q,V,K$ matrices, the architecture uses a combination of SSM (with diagonal and shift operations) and attention mechanism to produce the output.
$$ Q \odot SSM_{diag}(SSM_{shift}(K) \odot V)$$
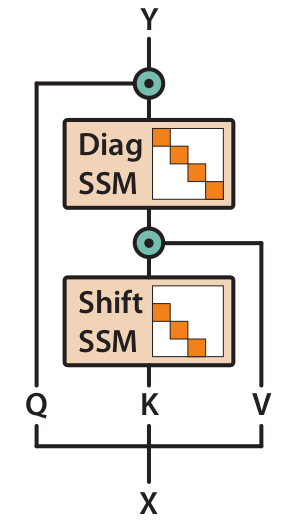
This allows for better handling of tokens after particular events, as the diagonal SSM addresses the ability to recall context, and the attention mechanism enables comparison of tokens. The resulting architecture could potentially have improved performance compared to either SSM or Attention alone, due to the combination of their strengths.
Shift SSM Link to heading
We constrain $A \in R^{m\times m}$ to be a shift matrix
$$A_{ij} = \begin{cases} 1 & \text{if } i-1 = j \ 0 & \text{otherwise} \end{cases} $$
By shifting the hidden state down by one we create a memory of previous states.
Diagonal SSM Link to heading
Constrains A to be diagonal initialized from a diagonal version of Hippo, this allows to remember tokens aftherwards for the rest of the sequence
Efficiency Link to heading
H3 scales $O(N \log N)$ for a sequence of length N where Attention requires $O(N^2)$ time and $O(N^2)$ space
Disclaimer Link to heading
I did read the original paper, and look at the code that was supplied with it. I did write this article on my own, however since I am not a native speaker, I did use ChatGPT for proof reading and improving my writing. If you are really interested how the original was worded. I will provide a link below.