Abstract Link to heading
State Space Models are awesome, models like Mamba and Mamba2 boast unparalleled performance especially when it comes to long sequences. The only downside is that they are causal, which means they model one token at a time, looking only at past tokens. Bidirectional models like Bert, CodeBERT and GraphCodeBERT have been shown to excel when it comes to code understanding. One way to put it is that by looking into the past and the future simultaneously we can get a better understanding of what is happening. Hydra is a bidirectional extension of Mamba2 that builds upon solid mathematical foundations, instead of just naively taking two Mamba(2)’s, flipping one of them, and somehow combining them.
Quasi-Separable Matrices Link to heading
We build upon research done in State Space Duality and the Mamba2 model. The main idea of Mamba2 is to express a State Space Model as:
$$ y = M \cdot x $$
- $M = SSS(A,B,C)$ is a Sequentially Semi-Separable Matrix
As a reminder, an N Semi-Separable Matrix is a lower triangular matrix where every submatrix contained in the lower triangular part is at most rank N. We can express any N Semi-Separable matrix as an N Sequentially Semi-Separable matrix. This just means that every entry in $M_{ij}$ is a product of vectors and matrices:
$$M_{ij} = C_j^A_j \cdots A_{i+1}B_i$$
- $B_0,\cdots, B_{T-1}, C_0, \cdots, C_{T-1} \in R^{N}$ are vectors
- $A_0, \cdots, A_{T-1} \in R^{N,N}$ are matrices
Since Semi-Separable matrices are lower triangular matrices, we can view them as a sort of causal attention mask. Since we are also interested in the future tokens, we need an matrix, that is non-zero above the main diagonal as well as below.
Definition Link to heading
Quasi-Separable Matrices consist of a lower and upper triangular matrix, with an special vector on the main diagonal.
$$ m_{ij} = \begin{cases} \xrightarrow[c_i^T ]{} \xrightarrow[A_{i:j}^x]{} \xrightarrow[b_j]{} && \text{ if } i> j \\ \delta_i && \text{ if } i = j \\ \xleftarrow[c_j^T ]{} \xleftarrow[A_{j:i}^x]{} \xleftarrow[b_i]{} && \text{ if } i<j \end{cases} $$
- $\delta_i$ is a scalar
- $b_i, c_i \in R^{N \times 1}$
- $A_i \in R^{N \times N}$
Here is an image so we can compare the two:

Hydra Link to heading
Right, so we know we need a Quasi-Separable Matrix, but how do we construct one? The answer is surprisingly simple, we just take two Semi-Separable Matrices and we masage them a bit.
$$QS(X) = \text{shift}(\text{SS}(X)) + \text{flip}(\text{shift}(\text{SS}(\text{flip}(X)))) + DX$$
- $SS$ is a semi-separable matrix, and in our case booth share the parameters ${A_i, b_i, c_i }_L$
- $D = \text{diag}(\delta_1, \cdots, \delta_L)$ are the diagonal parameters of the quasi-separable matrix
- $\text{flip}$ reverses the input
- $\text{shift}$ shifts the sequence to the right by one position, and pads the beginning with zeros
Model Link to heading
To get the intuition behind the model, we can look at the following pseudo code:
def hydra (
x , # (B ,L ,H*P)
A # (H ,) Parameter
):
x_b = flip (x , dim =1)
dt_f , dt_b = proj_dt (x) , proj_dt ( x_b ) # (B ,L ,H)
y_f = SSD( # (B ,L ,H*P)
x,
discretize_A (A , dt_f ) , # (B ,L ,H)
discretize_bc (x , dt_f ) , # (B ,L ,N)
)
y_b = SSD(
x_b ,
discretize_A(A , dt_b) , # (B ,L ,H)
discretize_bc(x_b, dt_b) , # (B ,L ,N)
)
y_f = shift(y_f , dim =1)
y_b = flip(shift(y_b , dim =1), dim =1)
y = y_f + y_b + x * repeat(
proj_D (x) ,
"B L H -> B L (H P)"
)
return y
- more on SSD
- the shift is required to make place for the diagonal entry of Matrix D
Here is the detailed description of a Hydra layer:
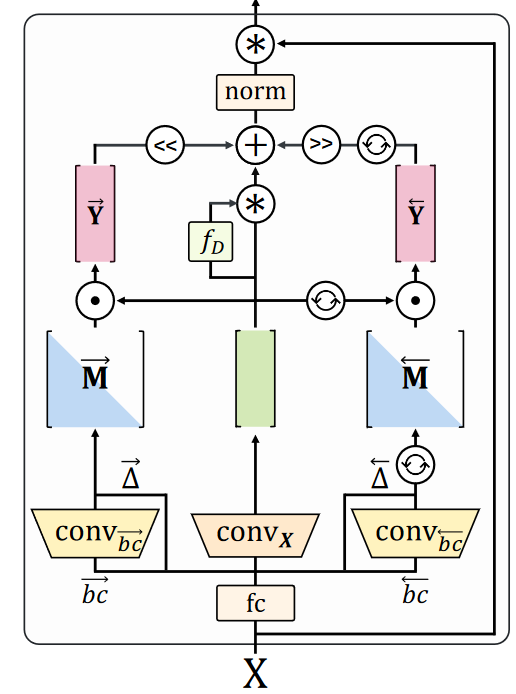
It is a bit (way) more involved, here is the actual [Source Code].
We have initial projections of the input, 1D convolutions, discretization, and flipping. We multiply it with the actual Semi-Separable matrix once for the forward and once for the backward direction. We do some elementwise product (selective gating), shifting, and merging the results together. That is followed by a normalization and a residual connection with the original input.
Pretraining Link to heading
Hydra uses the standard masked language modeling objective, where we mask out some tokens and try to predict them.
Remarks Link to heading
One thing that stands out is that the implementation, in comparison to BERT, is much more complex.
CLS Token Link to heading
The authors use a special pooling technique to average out the CLS token.
Efficiency Link to heading
It is worth mentioning that we share a single Semi-Separable matrix for the forward and backward direction. Because of this, Hydra introduces only a few more parameters (the diagonal matrix D) than Mamba2.
Unfortunately, the authors do not provide any empirical results on the runtime or memory usage of Hydra. But since it uses the same building block as Mamba2, we can expect it to give us gains especially on long sequences. I would like to see some benchmarks on the runtime and memory, especially compared to FlashAttention
Performance Link to heading
On the reported benchmarks, the performance of Hydra was higher than BERT across all tasks, with a couple of exceptions. Just having an alternative to bidirectional attention that is on par with BERT is a huge win.
Conclusion Link to heading
It is nice to see adaptation of SSMs also to bidirectional models. The research is only in its early stages, and only time will tell if Hydra will be applied in practice. There is a lot of research on hybrid models that combine State Space Models with Attention; especially the combination of Hydra and M2 could result in a powerful model that can handle extremely long sequences and still remain efficient.