Explore vs Exploit Link to heading
In reinforcement learning, we have an agent that has to take actions, for which it receives a reward. Here we have a dilemma: do we choose an action that gives the biggest reward or do we explore new actions that may lead to regions with even higher payouts?
Greedy Policy Link to heading
This is a simple one, we always take the option that gives us the highest payout:
$$ a_t = \arg \max_{a} Q(s,a) $$
The obvious downside is that we do not do any exploration. To fix this there are two possible extensions:
- $\epsilon$ Greedy policy $\pi_{\epsilon}$, this takes the greedy action as above with probability $\epsilon \in (0,1)$ otherwise we choose a random action. This is still not perfect since we equally explore all actions even if they are bad, however this can be solved by annealing $\epsilon \rightarrow 0$ with time.
- $\epsilon z$ Greedy policy. This is an extension of $\epsilon$ greedy where instead of making a single sample in the random direction we take multiple steps, the number of steps is determined by $n \sim z$ and it should help us to escape potential random minima we may get stuck in.
Boltzman Exploration Link to heading
Greedy policies above have the downside that they explore actions with equal probability. Boltzman exploration tries to fix it by exploring more promising actions with higher probability.
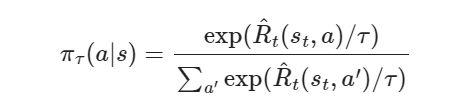
- $\tau > 0$ is a temperature parameter, as it gets closer to 0 we get a greedy distribution and with higher temperatures we get a more uniform distribution.
This is still not perfect, we explore different actions equally widely, which means that actions that we tried only a few times have some uncertainty in their actual payout. Because of this, we introduce an exploration bonus $R_t^b(s,a)$ which is higher for states we visited only a few times and decreases with each visit.
Optimal Explore-Exploit Strategy Link to heading
Is there an Optimal Explore-Exploit strategy? Well yes and no. Yes for some special types of models like Context-free Bandits which we can compute with dynamic programming, however for the general case this problem is not tractable.
Upper Confidence Bound and Thompson Sampling Link to heading
As mentioned above, optimal solution for explore-exploit tradeoff is not tractable, because of this we can introduce an optimistic estimate of the reward function: $\hat{R}$ which we call the upper confidence bound:
$$ \hat{R}_t(s_t,a) \ge R(s_t,a) $$
This function with high probability overestimates the payout for every action, then we greedily choose actions from this distribution:
$$ a_t = \arg \max_{a} \hat{R}_t(s,a) $$
This by itself would not do much, but we can imagine it as a uniform distribution where it overestimates everything by introducing an exploration bonus as in Boltzman Exploration (where with high temperature we get the same uniform distribution) for every action.
With time as we explore we continually decrease our optimism:
$$ \hat{R}_t - R_t $$
Thompson sampling Link to heading
It would be a sin to not mention Thompson sampling. It is a Bayesian approach, where we choose an action based on some probability, actions that have high payout are more likely to be chosen. Actions that we have not explored or explored only a little have high variance, thus making them still likely to be explored. Each time we take an action and get a reward we update our belief. We can also view it as assigning an extra probability to each state being optimal and we update this distribution as we sample.