Abstract Link to heading

We already know how to learn the Value function, however we also know that the Value function by itself is not enough since it averages over all possible actions, instead of taking into consideration specific actions the agent should take. We can derive the Q function from the Value function, however we can also try to directly learn it. Especially directly approximating the Q function with Deep Neural Networks has been a huge success when applied to RL Agents playing Atari computer games.

SARSA Link to heading

Sarsa is an on-policy method to learn the Q-function, thus it uses only the policy to choose the next action. Since it is an on-policy approach it may fail to learn the optimal policy $Q_{*}$, and later we are going to extend it to be off-policy, where we get stronger guarantees.

Equations Link to heading

$$Q(s, a) \leftarrow Q(s, a) + \eta [r + \gamma Q(s^{\prime}, a^{\prime}) - Q(s, a)] $$

This is just the Temporal Difference Learning, where the agent follows its policy $\pi$ at every step generating $a^{\prime} \sim \pi(s^{\prime})$ yielding the following $(s,a,r,s^{\prime}, a^{\prime})$ (hence the name SARSA).

Once we updated $Q$ we update the policy $\pi$ to be greedy with respect to $Q$.

Convergence Link to heading

The bad news, in the general case, SARSA is not guaranteed to converge to $Q_{*}$ however for the special, Tabular case (finite discrete states, finite discrete actions), in the limit that every state-action pair is visited infinitely often we are guaranteed to converge. Remember we are on-policy, and we update the Q function (and therefore the policy) only for action-state pairs which we actually visit! This can be done by performing $\epsilon$ greedy exploration-exploitation strategy with gradually vanishing $\epsilon \rightarrow 0$.

Off-policy Link to heading

As mentioned before SARSA is not guaranteed to converge, well actually Q learning has a lot of issues we are going to discuss later, but first things first. Off-policy approach enables us to use data, to train the agent from anywhere. This means we can use past training data, logs from some online system, imagination is the limit to train an RL Agent.

Tabular Q Learning Link to heading

We make the slightest modification to the SARSA training objective:

$$Q(s, a) \leftarrow Q(s, a) + \eta [r + \gamma \max_{a^{\prime}} Q(s^{\prime}, a^{\prime}) - Q(s, a)] $$

$a^{\prime} = \arg \max_{a}Q(s^{\prime}, a)$ replaces $a^{\prime} \sim \pi(s^{\prime})$

As before we need to visit every state-action pair at once, however since we use an off-policy approach: $(s,a,r,s^{\prime})$ can come from anywhere, which speeds up things!

Q-Learning as Function approximation Link to heading

Here our Q function has some parameters we are going to optimize: $Q_w(s,a)$, where $w$ are those parameters. These parameters are then usually optimized with Stochastic Gradient Descent and our loss is:

$$ L(w | s, a, r, s^{\prime}) = ((r + \gamma \max_{a^{\prime}} Q_w(s^{\prime}, a^{\prime})) - Q_w(s, a))^2$$

Deep Q Learning Link to heading

Here is not too much to say, essentially $w$ are weights of a deep neural network. This may sound disappointing, and yes it is. I wanted to dive more in depth here, and I’m going to give you a tease of the current latest and greatest at the end of the post. However I want to focus more on the problems and potential pitfalls that are present in Q learning!

Problems Link to heading

Off-policy methods and using Function approximation introduces a bunch of problems! These problems are:

The Deadly Triad
Optimizer’s Curse (Maximization Bias)

Deadly Triad Link to heading

In the context of Q-learning where we use Function Approximations (tabular case does not suffer from this, well it does, but it is less problematic), we may end up in a situation where the network is chasing its own tail. Let’s explain, essentially if we use TD learning, we use the Q function itself to estimate the new Q function, because of this we may end up in a situation that the algorithm is trying to adjust its estimate based on its own, potentially flawed estimate, creating a self-reinforcing feedback loop, causing divergence. There are actually 3 components, when we may experience instability during Q learning:

Using Function Approximations, since we use SGD to update the weights, if we have a biased state-action pair (or multiple) by updating the weights we influence all possible state-action pairs. In the tabular case the updates to one do not influence the other.
Using Bootstrapping, by using bootstrapping we do not minimize a fixed objective, we instead create a learning target using our own estimates. This can create a feedback loop pushing the estimates to infinity.
Using Off-policy Learning, since the data we use does not come from the policy that we optimize we may diverge from the policy we want to learn. In on-policy methods this is not an issue, since by optimizing the Q function we also optimize the learned policy creating a self-consistency feedback.

How to fix? Link to heading

Here are some of the methods:

Layer-norm, simply add a layer norm to the penultimate layer just before the linear head. This will force the weights $w$ to stay small, and it should be enough.
Target Networks

Target Networks Link to heading

Here we have 2 Q functions, $Q_{w^-}$ and $Q_{w}$, where we train only $Q_{w}$ and periodically we set $w^{-} \leftarrow sg(w)$, here sg is stop gradient. Essentially $w^{-}$ are frozen all the time!

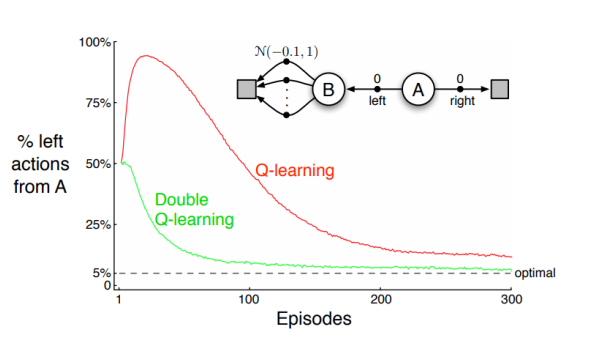
Optimizer’s Curse (Maximization Bias) Link to heading

There is non-trivial randomness involved in Q learning, since we use function approximations, we do not know the world model and actions $a$ we choose are stochastic. Because of this there is quite a chance that greedily picking an action that should pay most, we pick the wrong action due to random noise. This makes the learning way harder.

Double Q-Learning Link to heading

Double Q learning is an approach to avoid maximization bias where we have two separate Q-functions one is used to select a greedy action and the other for estimating the corresponding Q-value.

$$ Q_i(s, a) \leftarrow Q_i(s, a) + \eta (q_i(s, a) - Q_i(s, a)) $$ $$ q_i(s, a) = r + \gamma Q_i(s’, \underset{a’}{\text{argmax}} Q_{-i}(s’, a’))$$

For a given a transition tuple: $(s,a,r,s^{\prime})$ we use $Q_1$ to evaluate the action that $Q_2$ chooses.

And of course this can be applied to Deep Q learning as well.

Bigger, Better, Faster Link to heading

This relates to the BBF paper, which is the current benchmark for playing Atari games with Deep Q Networks (see we got there!). The authors propose the following tricks, ordered with decreasing importance:

Larger CNN: Use a larger CNN with residual connections, specifically a modified Impala network
Increase UTD Ratio: Increase the update-to-data (UTD) ratio (number of Q-function updates per observation) to improve sample efficiency
Soft Reset Weights: Periodically perform a soft reset of (some) network weights to prevent loss of elasticity, using the SR-SPR method
N-step Returns: Use n-step returns, gradually decreasing n from 10 to 3, to reduce bias.
Weight Decay: Add weight decay.
Self-Predictive Loss: Add a self-predictive representation loss to increase sample efficiency.
Increase Discount Factor: Gradually increase the discount factor (γ) from 0.97 to 0.997 to encourage longer-term planning.
Drop Noisy Nets: Remove noisy nets (as they increase memory usage without helping).
Dueling DQN: Use dueling DQN

In Dueling DQN we do not learn the Q function directly, but instead we learn a value function and advantage function and use them to derive the Q function.

Distributional DQN: Use distributional DQN

Distributional DQN predicts not just a single point estimate of the (discounted) return, but the whole distribution.

Final Remarks Link to heading

Q learning is popular and in some cases it is the state of the art solution, however as we are going to see in further posts, in some cases it may be advantageous to directly learn the agent’s policy, or even go down and learn the full model.