Source Link to heading

• Paper link: https://arxiv.org/abs/2406.05391
• Github Implementation: https://github.com/alipay/DUPLEX

Abstract Link to heading

I am a huge fan of Graph Machine Learning, it has a lot of cool applications, and I am particularly interested in Source Code understanding and Vulnerability Detection, where Graph Neural Networks (GNN) are unambiguous. One of the obvious downsides of general GNNs is that they mostly focus on undirected graphs, which makes their approach somewhat limiting for Digraphs (fancy name for directed graphs). This TLDR; is about DUPLEX (I already wrote about its application in GaLLa) which is a cool technique to learn node representations in a self-supervised way (can be extended with arbitrary objectives).

TLDR; DUPLEX Link to heading

It is a technique for Digraphs where we learn low-dimensional Node representations that can be used for downstream tasks. To fully capture the directionality and the information flow we make the learned Node representations complex valued and we learn them with a dual Graph Attention Network (GAT) encoder. We then reconstruct the learned complex node embedding using two parameter-free decoders.

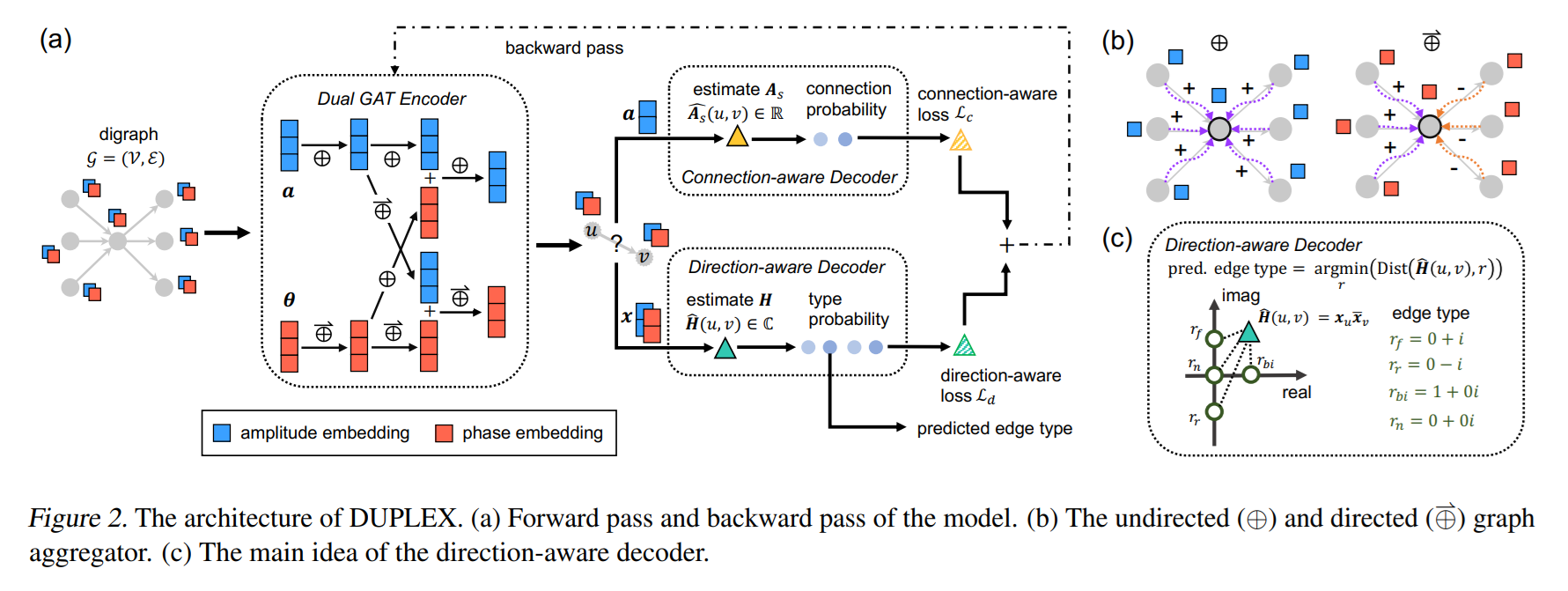
Hermitian Adjacency Matrix (HAM) Link to heading

Normally we can use the Adjacency matrix of a Graph to describe the connection (edges) between nodes, however this does not tell us anything useful about the direction of these edges. To capture the direction we are going to use Hermitian Adjacency Matrix (HAM) where its entry for a pair of nodes $u,v$ is $H_{u,v} \in { i, -i, 1, 0}$ which represents a forward, reverse, bidirectional and no edge between these nodes.

$$ H = A_s \odot \exp(i \frac{\pi}{w} \Theta)$$

• $i$ is the imaginary unit
• $\pi$ is just 3.14…… pi :)
• $\odot$ is the Hadamard (element wise) product
• $A_s$ is the undirected symmetric Adjacency matrix

$$ \Theta(u, v) = \begin{cases} 1, & \text{if } (u, v) \in \mathcal{E}, \\ -1, & \text{if } (v, u) \in \mathcal{E}, \\ 0, & \text{otherwise} \end{cases}$$

So the HAM can represent all the possible link directions, but it can also be decomposed as:

$$H = X^T \tilde{X}$$

$$x_{u} = a_{u} \odot \exp (i \frac{\pi}{2} \theta_{u})$$ $$\tilde{x_u} = a_{u} \odot \exp (-i \frac{\pi}{2} \theta_{u}) $$

• $a_u$ is the amplitude and $\theta_u$ is the phase of $x_u$
• $x_u \in C^{d \times 1}$ is complex embedding and $\tilde{x}_u$ is its complex conjugate

Now what we want is to learn for each node is to learn $a_u$ and $\theta_u$ from which we can then construct the complex embedding!

Dual GAT Encoder Link to heading

From above it should be obvious we need:

1. Amplitude Encoder
2. Phase Encoder

Both of them will use GAT under the hood for message passing and we need an extra Fusion Layer to share information between them.

Amplitude Encoder Link to heading

Here we learn an embedding $a_u$ for node $u$, which captures only the connection information (we do not care about the direction)

$$ a_{u}^{\prime} = \phi (\sum_{v \in \mathcal{N}(u)} f_a(a_{u}, a_{v}) \psi_a(a_{v} ) )$$

• $N(u)$ is the neighborhood of u
• $\phi$ is the activation function here we use ReLU
• $f_a, \psi_a$ is the learnable attention mechanism

Phase Encoder Link to heading

We learn an embedding $\theta_u$, the approach is similar to amplitude but with the difference that here we care about the direction information.

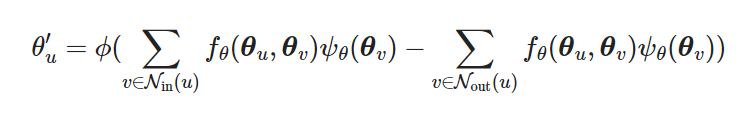
• the important difference is that there is a subtraction between the in-neighborhood information and out-neighborhood information, this is due to their asymmetry

Fusion Layer Link to heading

We combine the information from the amplitude and phase embedding to update the amplitude embedding (only)

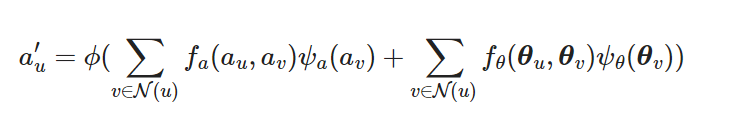
• just a sum of two attention layers passed through a non-linearity, the first GAT derives the key using the amplitude embedding and the second uses phase embedding as key, in both cases we take the whole node neighborhood into account discarding the direction information

This is an example of “mid-fusion”, where we integrate embeddings at the network’s intermediate layers. We do this instead of early fusion because if there are no node attributes it would introduce only random noise and late-fusion (at the terminal layer) can dilute the unique attributes of the amplitude and phase embeddings.

Notes Link to heading

We technically can replace GAT with any other Spatial GNN, also Mamba!

Two Parameter free Decoders Link to heading

We learned an amplitude embedding $a_u$ and a phase embedding $\theta_u$ which we can use to construct the complex embedding $x_u$. From these 3 embeddings (well actually we only use $x_u$ and $a_u$) we are going to train two decoders:

1. Direction aware Decoder
2. Connection aware Decoder

Each has its own supervised loss function, with the total loss of the model defined as the sum of individual losses $\mathcal{L} = \mathcal{L}_d + \lambda \mathcal{L}_c$.

Direction aware decoder Link to heading

This decoder focuses on reconstructing the complex-valued HAM of the Digraph:

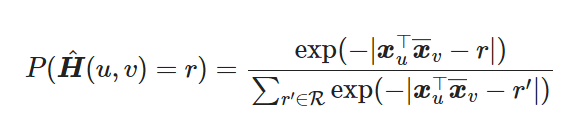
• this calculates the probability of having an edge between (u,v) and the edge type $r$

With the loss is defined as:

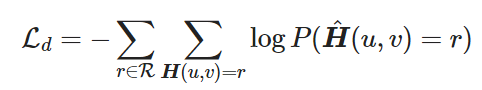
• here $x_u, \bar{x}_u$ are node embeddings in polar form

Connection aware decoder Link to heading

This decoder focuses only on the existence of connections, it can be viewed as an auxiliary to the Direction aware decoder:

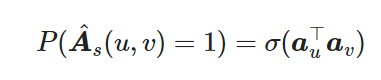
• $\sigma$ is the sigmoid function with $\hat{A}$ is the estimated undirected Adjacency matrix

• the loss is the same negative sum log likelihood as in direction aware.

Final Remarks Link to heading

First of all, in terms of performance it is state of the art when it comes to Digraphs (most papers are! at least during the time of their publishing). The biggest benefit is using GAT for the encoders, this gives a huge benefit since it is enough to aggregate neighborhood information making the model scale to graphs that are similar to the ones inside the training set. Second, the self-supervised method allows pretraining in absence of any labeled data and we can then build models on top of these representations, where we concatenate the phase and amplitude embedding. In case we have labels we can easily extend the learning objective to take them into account!