Bayes rule¶
To derive the bayes rule first we start with joint and conditional distribution.
\(p(A|B)\) is the probability that event A will happen given that we know that B has happended.
\[
p(A|B) = \frac{p(A,B)}{p(B)}
\]
\(P(A,B)\) this tells us the probability that booth A and B have happend.
\(p(B)\) is a normalization constant. (But it has happend)
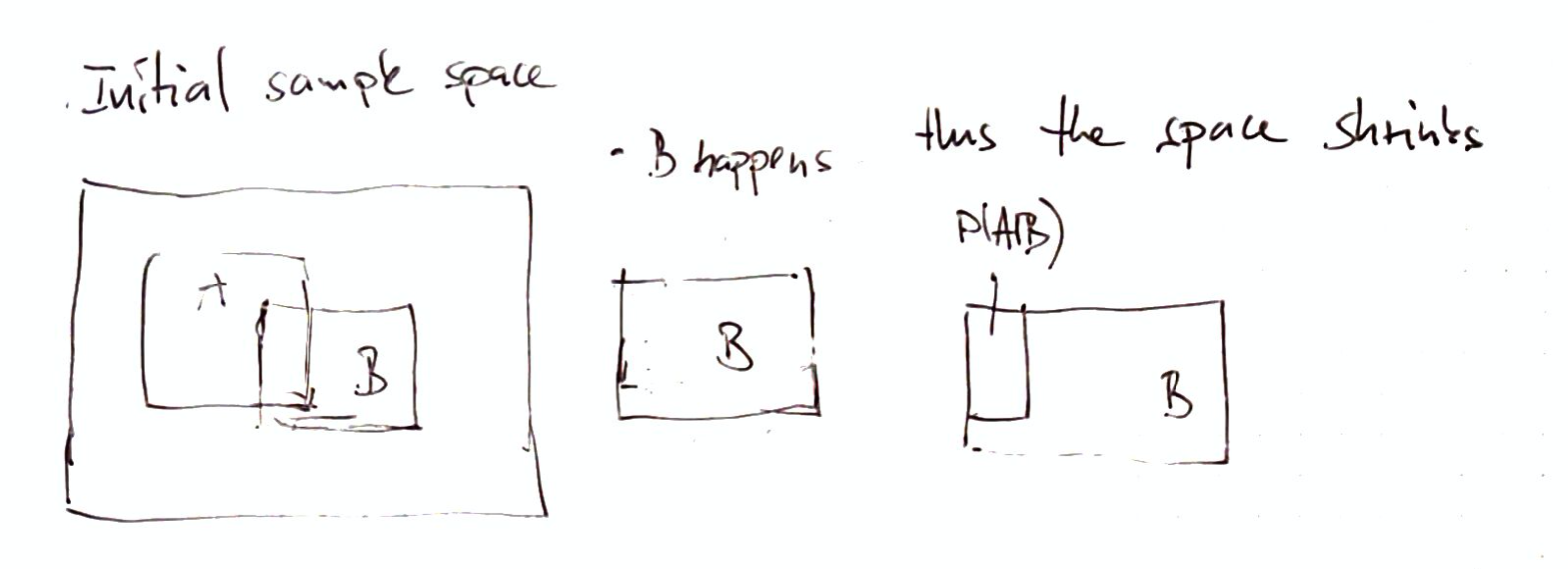
Now we can express this the other way:
\[P(B|A) = \frac{p(B,A)}{p(A)}\]
The joint distribution is simetric:
\[
p(A,B) = p(B,A)
\]
Now we can rearange the terms:
\[\begin{split}
p(A,B) = p(B,A) \\
p(A|B)p(B) = p(B|A)p(A) \\
p(A|B) = \frac{p(B|A)p(A)}{p(B)}
\end{split}\]
And we have drived the bayes rule.
