Contents

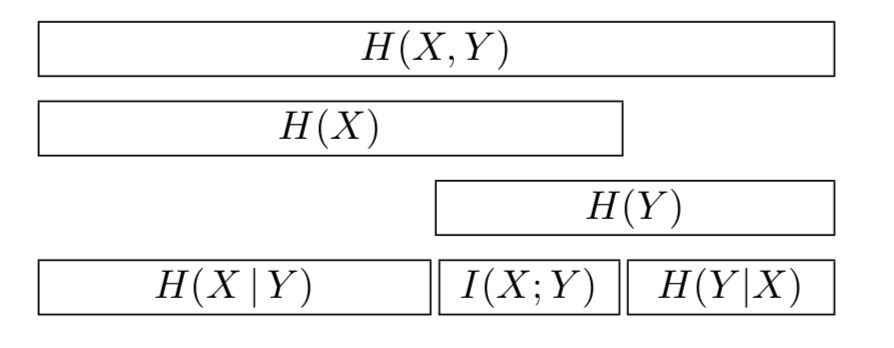
Mutual information¶

Given 2 random variables \(X\) and \(Y\) we may ask, if we know X how much knowledge we gain about Y. We can achieve this by comparing the KL Divergence the joint distribution \(p(X,Y)\) with the factored distribution \(p(X)p(Y)\).

\[ I(X;Y) \triangleq KL(p(X,Y)||p(X)p(Y)) = \sum_x \sum_y p(x,y) \log \frac{p(x,y)}{p(x)p(y)} \]

  • This is always positive

  • \(I(X;Y) = 0\) only if \(p(X,Y) = p(X)p(Y)\)

ONLY defined for discrete random variables

Entropy¶

Mutual information can be expressed using entropy:

\[ I(X;Y) = H(X) - H(X|Y) = H(Y) - H(Y|X) \]

  • \(H\) is the entropy

  • \(H(Y|X) = \sum_x p(x)H(Y|X=x)\) is the conditional entropy

This can be interpreted as the reduction in uncertainity about X after observing Y (And vice versa)

mutual information

Point wise mutual information¶

This defines MI between two events (not random variables).

\[PMI(x,y) \triangleq \log \frac{p(x,y)}{p(x) p(y)} = \log \frac{p(x|y)}{p(x)} = \log \frac{p(y|x)}{p(y)}\]

Measures the discrepancy between these events occuring together \((p(x,y))\) compared to what would be expected by chance \((p(x)p(y))\) (they are independent).

Alternatively we can view it as the amount we learn from updating the prior \(p(x)\) into the posterior \(p(x|y)\). (\(\frac{p(x|y)}{p(x)}\))

Continuous random variables¶

We have to discretize them first. Unfortunately this involves choosing the number of bins, and finding their boundaries.

There is an approach, maximal information coefficient (MIC), which tries many different bin sizes and lcoations to compute the maximum MI achieved.

Gaussian Process <no title>