Jensens inequality¶
If we take expectations for a function the following holds:
\[
E[g(X)] \ne g(E[X])
\]
However if \(f\) is a convex function than we can prove that:
\[E[g(X)] \ge g(E[X]) \]
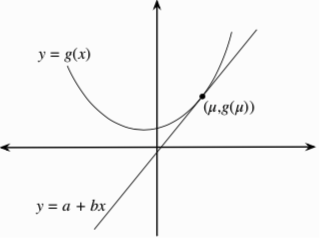
Prof¶
\[E[g(x)] \ge E[a + bX] = a + bE[X] = a+b\mu = g(\mu) = g(E[X]) \]
Concave functions¶
\[
E[g(X)] \le g(E[X])
\]
