Rejection sampling¶
We assume that \(P(x) = P^*(x)/Z\) is too complicated to draw samples directly. And we assume we have a simpler proposal density \(Q(x)\) which we can evaluate (within a multiplicative factor \(Z_Q\)), and from which we can draw samples. Further we assume that we know the value of a constant c such that:
\[ cQ^{*}(x) > P^*(x) \text{, for all x}\]
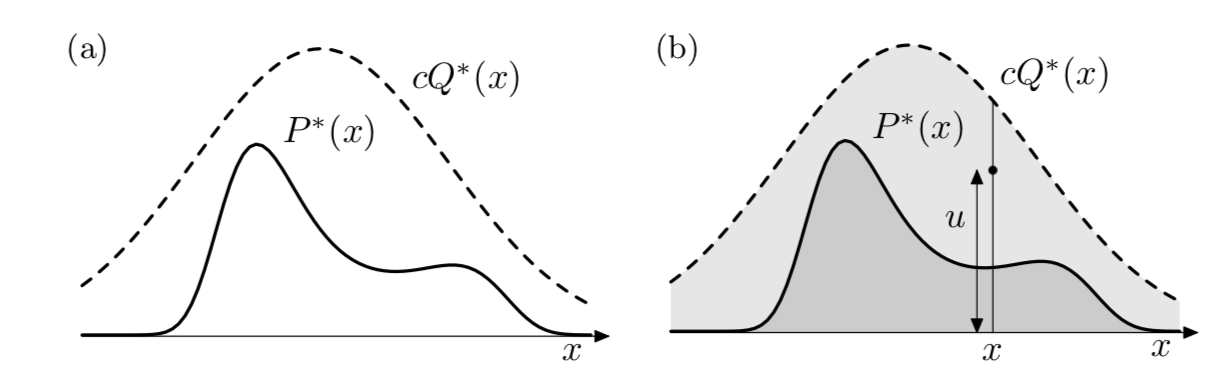
After that we generate a uniformly distributed random variable from the interval \([0, cQ^*(x)]\). Now we compare u to \(P^*(x)\). If \(u > P^*(x)\) then we reject x otherwise we accept it.
Rejection sampling works best if Q is a good approximation of P. And we need to choose \(c\) to be as small as possible.
Remarks¶
In high dimensions we have to set \(c\) to be large, which will make the acceptance ration rare. Thus it will take ages.
