Quadratic discriminant analysis (QDA)¶
Can be used for classification where we assume each class is drawn from its Gaussian distribution. This yield an quadratic decision boundary:
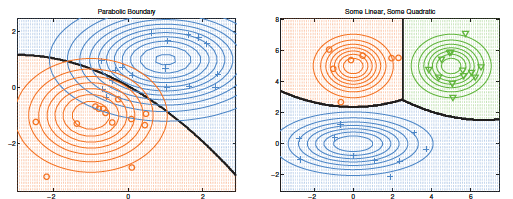
\[p(y=c| x, \theta) = \frac{\pi_c |2\pi \Sigma_c|^{-1/2} \exp {[- \frac{1}{2} (x- \mu_c)^T \Sigma^{-1}_c (x-\mu_c) ]}}{\sum_{c'} \pi_{c'} |2\pi \Sigma_{c'}|^{-1/2} \exp {[-\frac{1}{2} (x- \mu_{c'})^T \Sigma^{-1}_{c'} (x-\mu_{c'}) ]}}\]
\[
p(y=c|x, \theta) = \frac{N(x|\mu_c, \Sigma_c)}{\sum_c' N(x|\mu_c, \Sigma_c)}
\]
\(\pi_c\) is the class Prior \(\sum_c \pi_c = 1\)
\(\mu_c, \Sigma_c\) is the mean and variacne of class \(c\)$$
