Sum-product message passing¶
It is an variant of belief propagation used to compute marginals.
Algorithm¶
While there is a node \(x_i\) ready to transmit to \(x_j\) it sends the message:
\[
m_{i \rightarrow j}(x_j) = \sum_{x_i} [\phi(x_i)\phi(x_i,x_j) \prod_{l \in N(i)\backslash j} m_{l\rightarrow i}(x_i)]
\]
\(N(i)\backslash j\) set of nodes that are neighbors of i excluding j.
This message is just the factor \(\tau\) that \(x_i\) would transmit to \(x_j\) during variable elimination if the goal would be computing \(p(x_j)\).
We can use the computed messages to answer any marginal query over \(x_i\):
\[
p(x_i) \propto \phi(x_i) \prod_{l \in N(i)} m_{l \rightarrow i} (x_i)
\]
Example¶

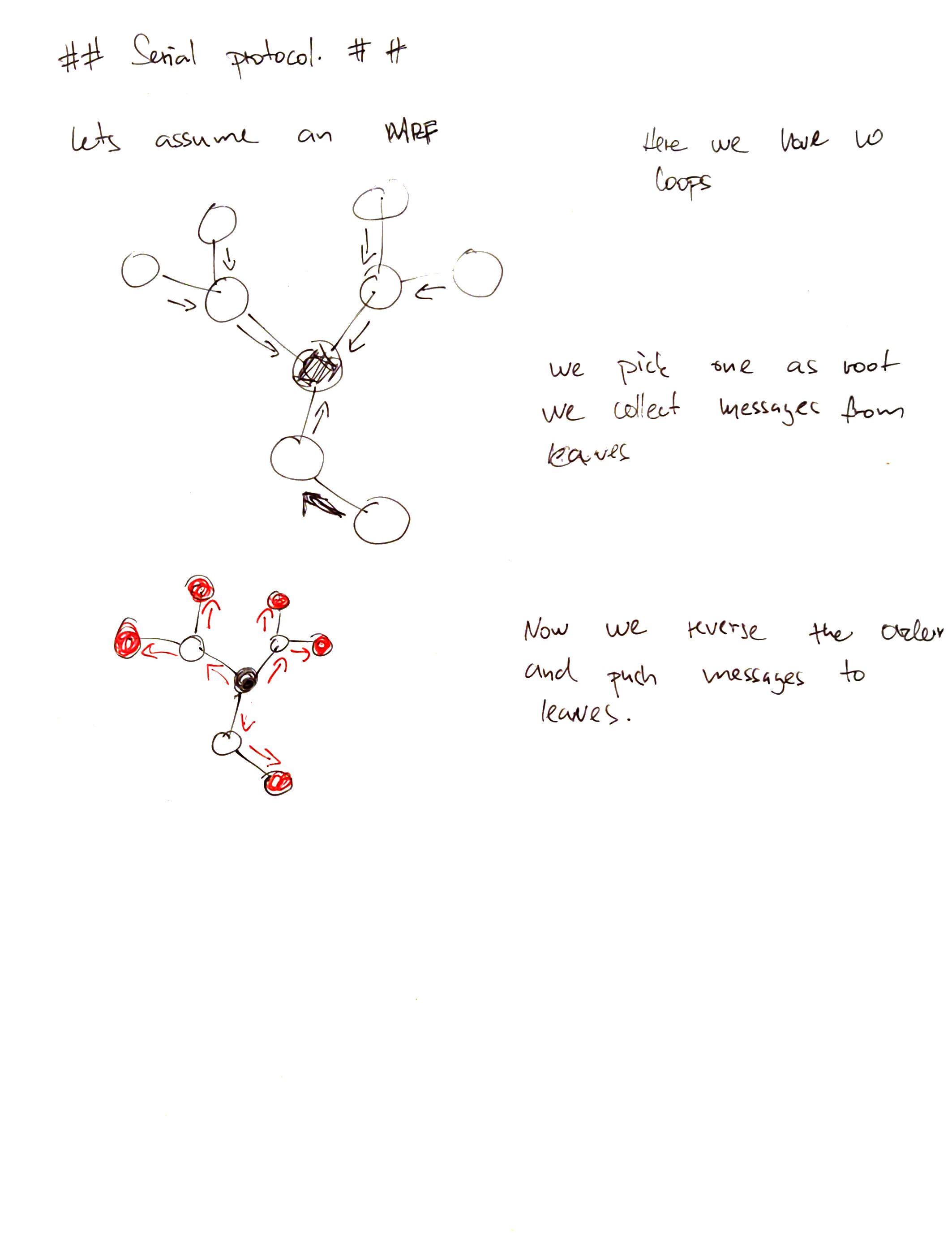
Serial protocol¶
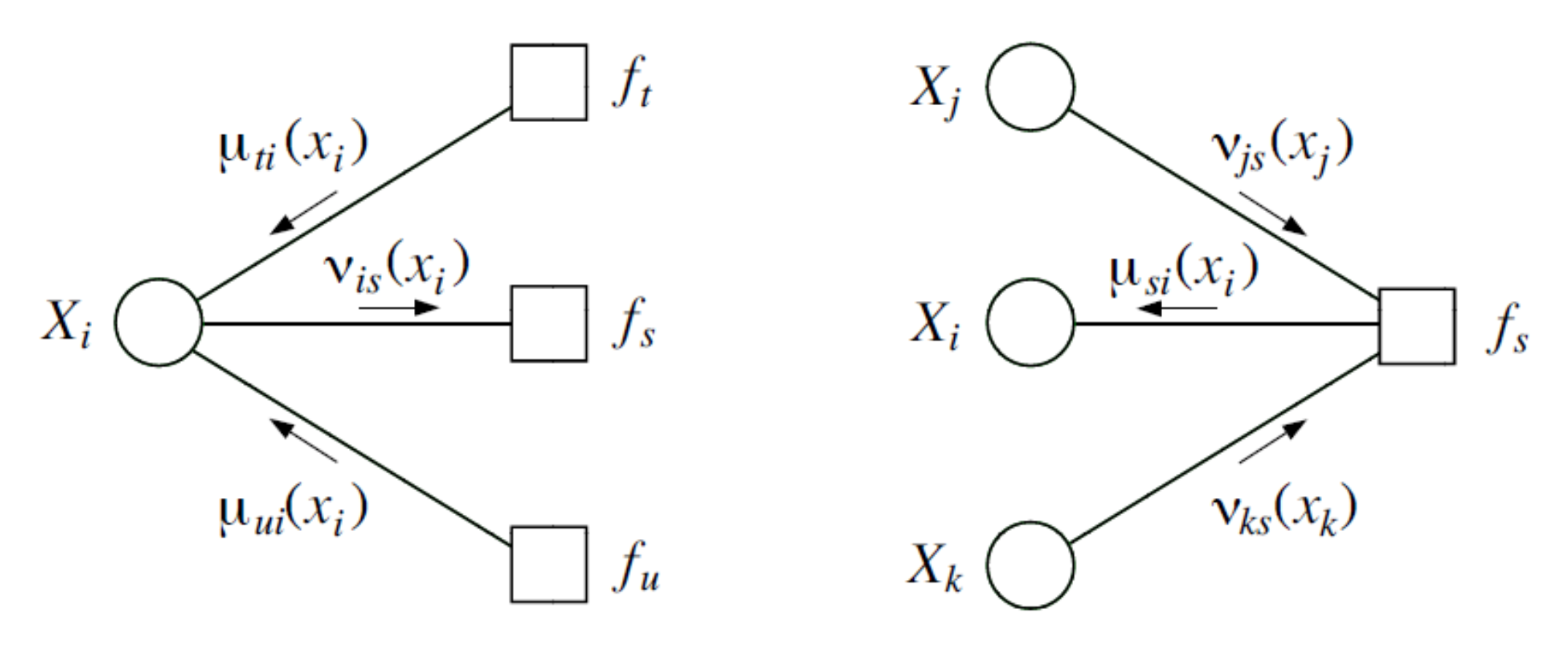
Algorithm for factor trees¶
We apply message passing to factor trees. In factor graphs we have two type of messages.
variable-to-factor message \(v\)
factor-to-variable message \(\mu\)
\[\begin{split}
v_{\text{var}(i)\rightarrow \text{fac}(s)}(x_i) = \prod_{t \in N(i)\backslash s} \mu_{\text{fac}(t) \rightarrow \text{var}(i)}(x_i) \\
\mu_{\text{fac}(s) \rightarrow \text{var}(i)}(x_i) = \sum_{x_{N(s)\backslash i}}f_s(x_{N(s)}) \prod_{j \in N(s)\backslash i} v_{\text{var}(j) \rightarrow \text{fac}(s)}(x_j)
\end{split}\]