Acceleration¶

If the velocity of a moving object changes with time, we say that the object has acceleration.Acceleration is a quantitative description of the rate of change of velocity with time. In general we divide an change in velocity by time. Thus this is again an vector quantity.

Units¶

\[ \frac{(m/s)}{s} = m/s^2 \]

They are in meters per second sequared.

Average acceleration¶

\[ a_{av,x} = \frac{\Delta v_x}{\Delta t} \]

It is the difference between velocity divided by time. This difference can be negative if we are deaccelerating. Thus the velocity decreases.

Instantaneous acceleration¶

\[ a_{x} =\lim_{\Delta t \rightarrow 0} \frac{\Delta v_x}{\Delta t} \]

It is the acceleration at any given time or point along the path. In general if we talk about acceleration we think about instantaneous acceleration.

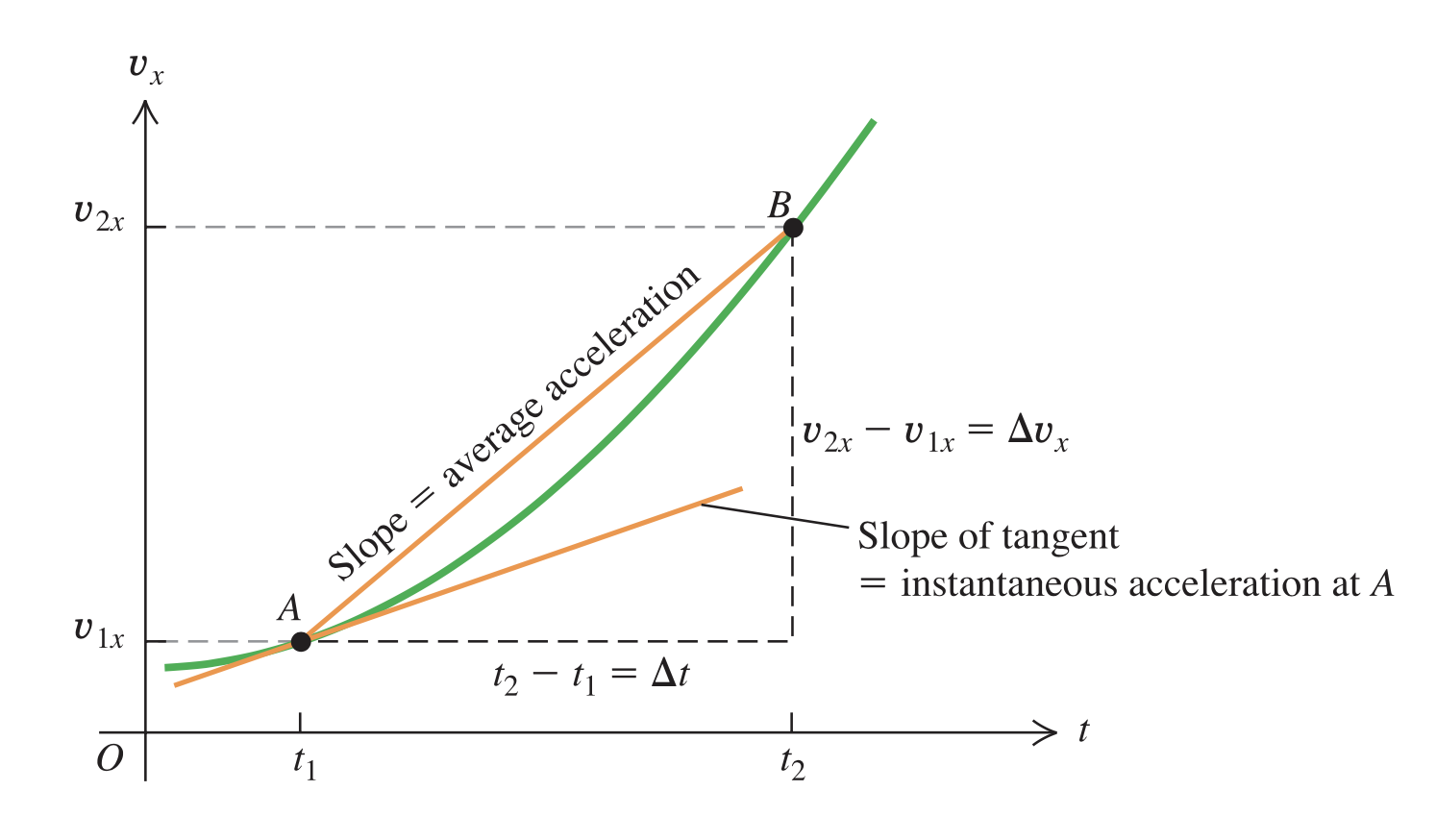
We can express acceleration as a function of t.

The average acceleration between any two points on a graph of velocity versus time equals the slope of a line connecting those points. The instantaneous acceleration at any point on the graph equals the slope of the line tangent to the curve at that point.

Motion with contant accelration¶

The instantaneous acceleration does not change.

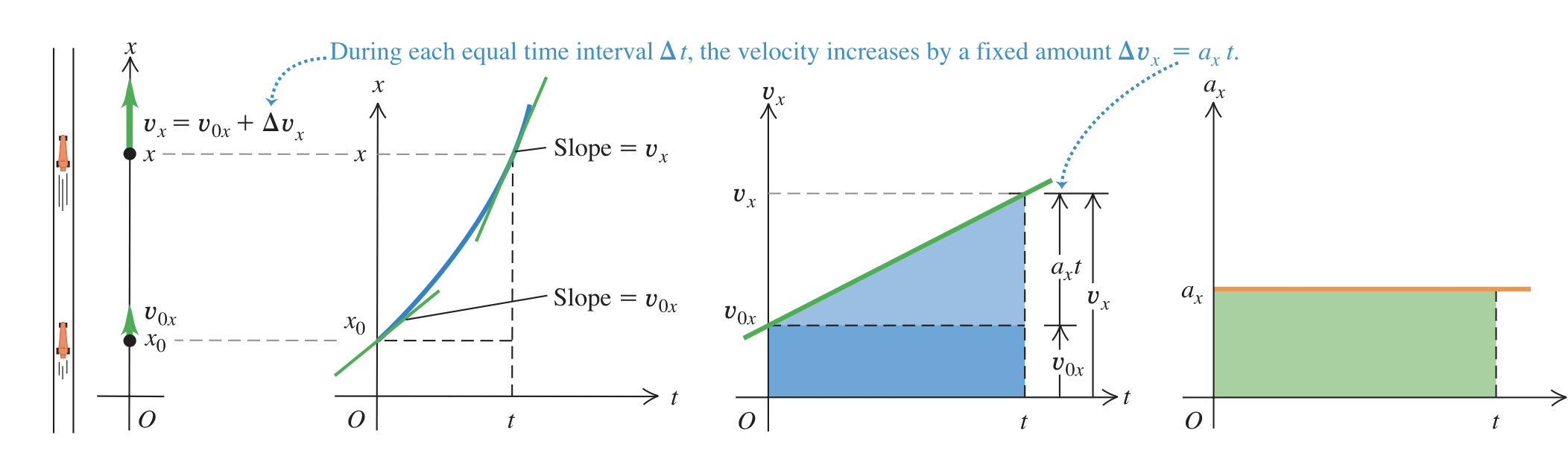
The change in velocity is a linear curve. The velocity after accelerating is:

\[\begin{split} a_x = \frac{v_x - v_{0x}}{t-0} \\ v_x = v_{0x} + a_x t \end{split}\]

Thus it is the initial velocity plus, t times the acceleration.

If the acceleration is constant we can calculate the average velocity:

\[\begin{split} v_{av,x} = \frac{v_{0x} + v_x}{2} \\ = \frac{1}{2} (v_{0x} + v_{0x} + a_xt) \\ = v_{0x} + \frac{1}{2}a_xt \\ = \frac{\Delta x}{\Delta t} \end{split}\]

If \(\Delta t = t - 0\) (we start at t = 0) we can simplify to:

\[ v_{av,x} = \frac{x-x_0}{t} \]

Position afther constant acceleration¶

We can put the equations together do derive:

\[\begin{split} v_{0x} + \frac{1}{2}a_xt = \frac{x - x_0}{t} \\ x = x_0 + v_{0x}t + \frac{1}{2} a_xt^2 \end{split}\]

If we express \(t = \frac{v_x - v_{0x}}{a_x}\) (the time we need reach the target velocity under acceleration \(a_x\)). Now we can express the distance traveled as:

\[\begin{split} x = x_0 + v_{0x} (\frac{v_x - v_{0x}}{a_x}) + \frac{1}{2}a_x (\frac{v_x - v_{0x}}{a_x})^2 \\ 2a_x(x - x_0) = 2v_{0x} v_x - 2v_{0x}^2 + v_x^2 - 2v_{0x}v_x + v_{0x}^2 \end{split}\]

This can be simplified into:

\[ v_x^2 = v_{0x}^2 + 2a_x(x - x_0) \]

Free falling¶

It is the acceleration due gravity, on earth this is:

\[ a = -g = 9.8m/s^2 \]

study-notes