Sigmoid and Softplus¶
Sigmoid¶
The sigmoid function can transform an interval form \(-\infty, \infty\) to be between \(0, 1\)
\[\begin{split}
\delta(x) = \frac{1}{1+\exp(-x)} = \frac{\exp(x)}{\exp(x) + \exp(0)} \\
0 \le \delta(x) \le 1 \space \text{ for } -\infty \le x \le \infty
\end{split}\]
Properties¶
\[ \begin{align}\begin{aligned}\begin{split}
\frac{d\delta}{d x} = \delta(x) (1 - \delta(x)) \\
1 - \delta(x) = \delta(x) \\\end{split}\\\forall x \in (0,1), \space \delta^{-1}(x) = \log (\frac{x}{1-x})
\end{aligned}\end{align} \]
\(\delta^{-1}\) is the logit function
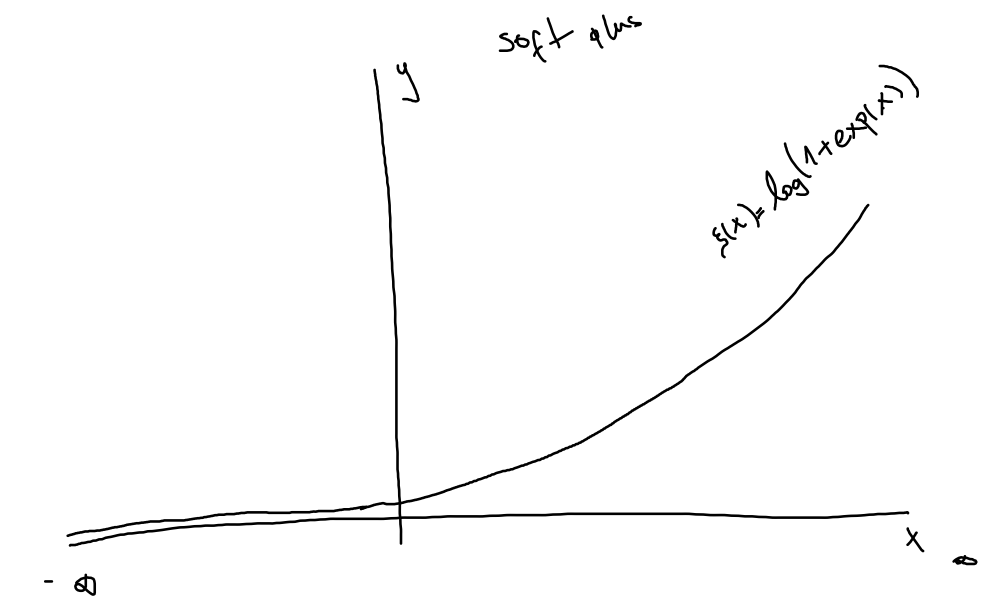
Softplus¶
It is the soft of the max function \(x^+ = max(0,x)\) $\( \xi(x) = \log(1 + \exp(x)) \\ 0 < \xi(x) \le \infty \)$
Properties¶
\[\begin{split}
\frac{d}{dx} \xi (x) = \delta(x) \\
\forall x > 0, \space \xi^{-1}(x) = \log (\exp(x) -1) \\
\xi(x) - \xi(-x) = x
\end{split}\]
Relationship between softplus and sigmoid¶
\[\begin{split}
\log \delta(x) = - \xi (-x) \\
\xi(x) = \int^x_{-\infty} \delta(y)dy
\end{split}\]
