Search Trees¶

The basic functionality of a search tree is:

M[k] finding an element by a key, or throwing an error if it does not exists
M[k] = v Associate a value v with key k in map M. (or replace)
del M[k] Remove from map M the item with key equal to k. Raise an error if k is not contained.

Binary Search Tree¶

Binary trees are excellent for storing items of a map, assuming that the kays can be ordered. The binary search tree satisfies that:

Keys stored in the left subtree of p are less than k
Keys stored in the right subtree of p are greater than k

In this tree we can perform an binary in order traversal, thus we visit each position in increasing order of their keys.

Searching¶

Runs in O(h), h is the depth of the search tree.

Insertion¶

In case that we find an element we just replace it. If we fail to find the element, the search ends at a leaf.

Algorithm TreeInsert(T, k, v):
    Input: A search key k to be associated with value v
    p = TreeSearch(T,T.root(),k) 
    if k == p.key() then
        Set p’s value to v 
    else if k < p.key() then
        add node with item (k,v) as left child of p 
    else
        add node with item (k,v) as right child of p

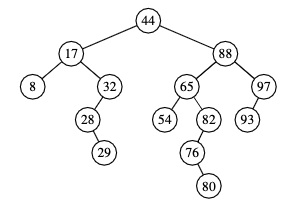
Here we insert 68 into a search tree:

Deletion¶

Deletion may happen anywhere in the tree. First we need to find the position \(p\) of the element we want to delete. If we find it there are two general cases:

\(p\) has at most one child, than we delete p and replace it with its child.
\(p\) has two children
1. We locate position r that is greatest key that is strictly less than at position \(p\) (the right most postion of the left subtree of \(p\))
2. We use \(r\) as a replacement for the one being deleted at position p
3. Since r is the right most position in the subtree, it wont have a right child, therefore we can just simply delete \(r\)

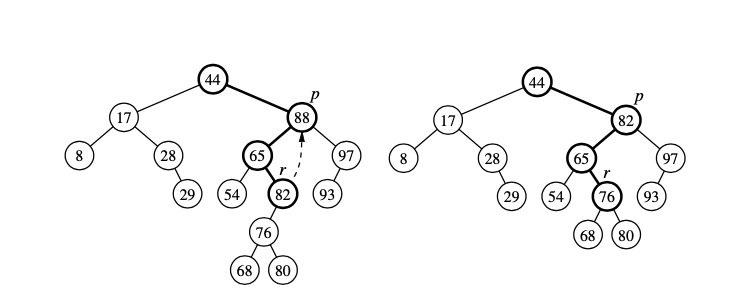
Here we delete 88.

Balanced search trees ¶

The naive search tree provides O(n) worst case performance, thus we turn to a data-structure that has stronger guarantees. In general we need to keep the tree balanced, or to keep its height equal \(h=[\log (n+1)] - 1\).

study-notes