Gamma distribution¶

Gamma distribution can be viewed as the total waiting time, till we reach $a$ successes. It generalizes the Exponential r.v, where the Exponential r.v is the waiting time for the first success under condition of memorylessnes. We can view the Gamma distribution as a sum of i.i.d Exponential r.v.s. Of we can see the Gamma as the continuous analog of the Negative Binomial distribution.

\[X \sim Gamma(a,\lambda)\]

PDF¶

In terms of shape $(k)$ and scale $(\theta)$

\[f(x| k, \theta) = \frac{1}{\theta^k} \frac{1}{\Gamma(k)}x^{k-1} e^{-\frac{x}{\theta}}\]

In terms of shape ($\alpha$) and rate ($\theta$)

\[ f(x| \alpha, \beta) = \beta^{\alpha} \frac{1}{\Gamma(\alpha)}x^{\alpha -1} e^{-\beta x}, x> 0, \text{ and } \alpha, \beta> 0\]

Moments¶

Mean¶

$E[X] = \frac{a}{\lambda}$

Variance¶

$Var(X) = \frac{a}{\lambda^2}$

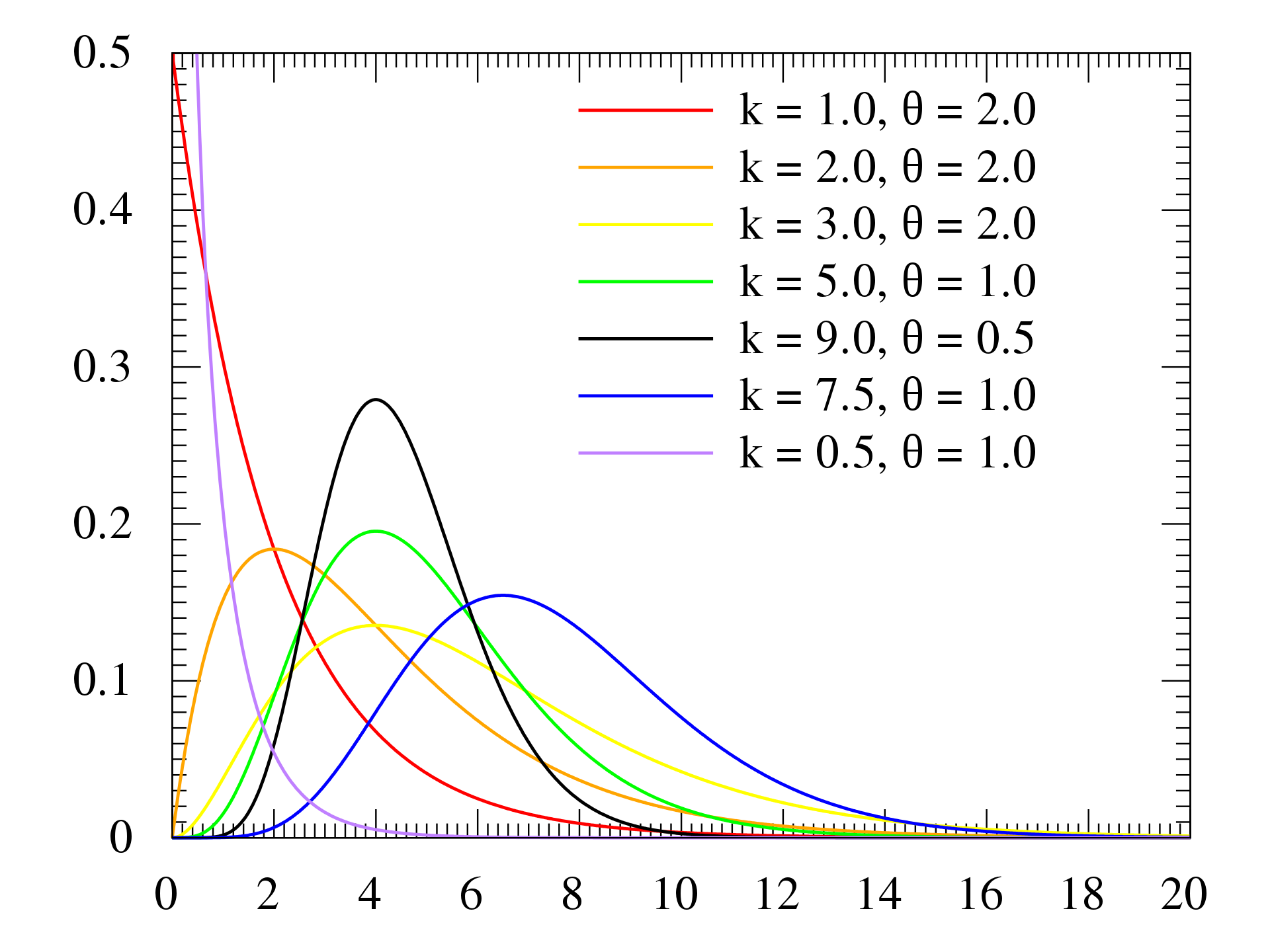
Properties¶

the shape parameters defines the number of events (thus it can be any positive number)
- shape values less than 1, Gamma distribution has a mode of 0
- shape value equal to 1, gamma distribution is equivalent to exponential distribution
- shape values greater than 1, the distribution becomes increasingly more symmetrical and approaches a normal distribution when the shape parameter is large.
The scale and rate (rate = 1/scale) parameter defines how often (scale) and rate at which events are expected to occur
The variance is proportional to the mean (variance = scale/mean, variance = mean^2/ shape)

Sum of 2 Gamma distributions¶

If 2 or more gamma distributions have the same rate $\alpha$

$X \sim Gamma(a, \lambda)$
$Y \sim Gamma(b, \lambda)$

Then we can define the sum of 2 or more as:

\[T = X + Y \sim Gamma(a+b, \lambda)\]

Connection to Exponential distribution¶

And since there is a connection between the Exponential and Gamma:

\[X \sim Gamma(1, \lambda) = Expo(\lambda)\]

Connection to Beta distribution¶

\[\frac{1}{\beta(a,b)} = \frac{\Gamma(a + b)}{\Gamma(a)\Gamma(b)}\]

$\Gamma$ is the gamma functiin

Connection to Normal distribution¶

Gamma distribution can be used as an alternative to Normal distribution when data (residuals) are skewed with a long right tail, when there is an relationship between mean and variance.

It is a conjugate prior for the variance of a normal distribution.

Erlang distribution¶

Parameter $a$ is a integer, which is commonly fixed yielding a one parameter Erlang distribution, $$Erlang(x| \lambda)= Ga(x| 2, \lambda)$$

fix $a = 2$)
$\lambda$ is the rate parameter.

Bayes factors Exponential distribution

study-notes