Projectile Motion¶

Here we simplify a bit, we ignore the curvature and air resistance.

Here we assume that the acceleration towards earth is constant:

\[ a_y = -g \]

The vertical and horizontal motions are independent, that means if we throw two balls, one straight to the ground the other with some velocity to the side they booth reach ground at the same time.

Thus we need to trait the x and y coordinate separately.

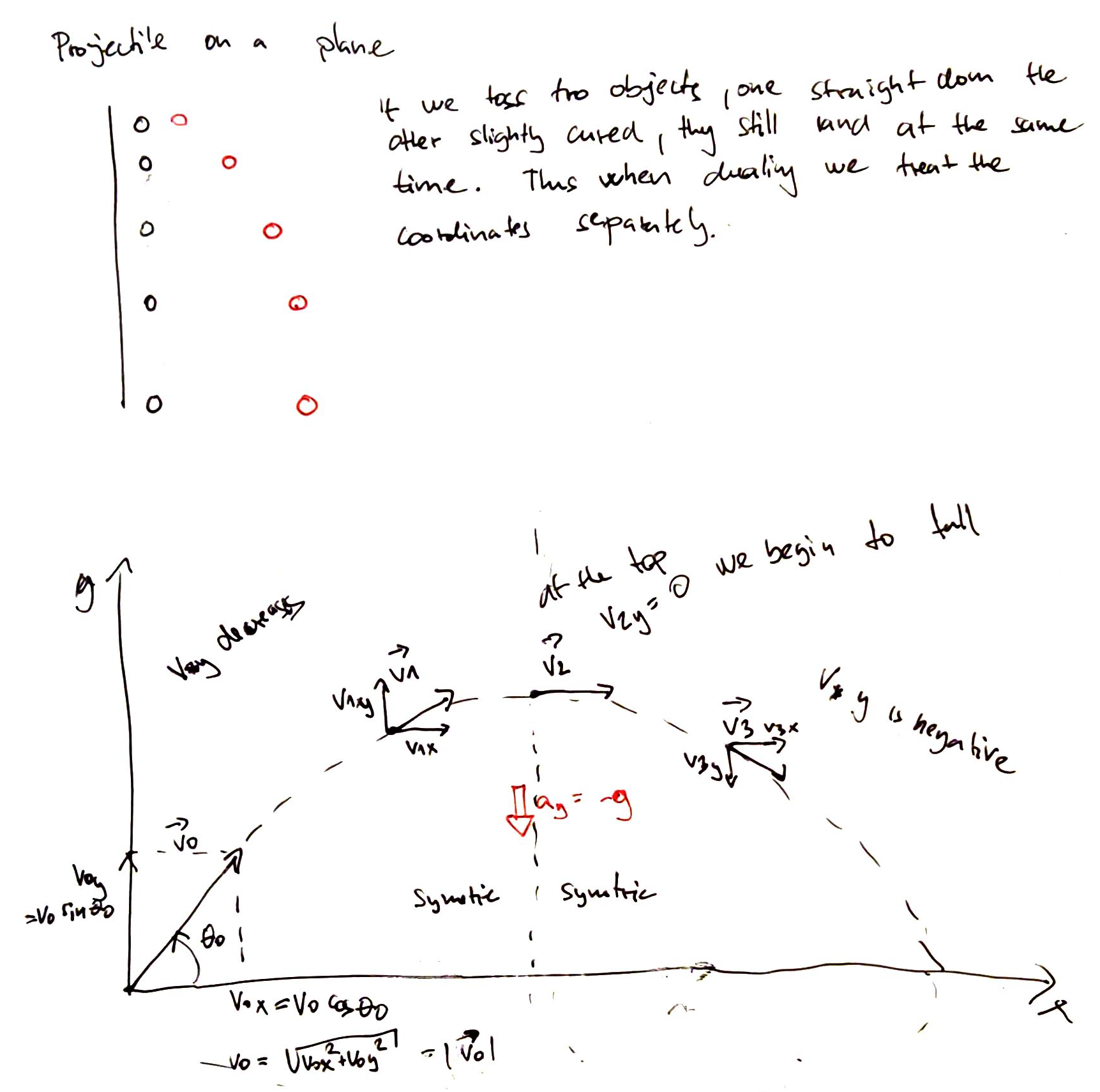
In projectile motion booth the horizontal and vertical axis wary with constant acceleration. (Horizontal component of acceleration is constant at zero.)

The acceleration of a projectile is zero, thus $v_x$ is constant, but $v_y$ changes by constant acceleration (gravity). At the highest point $v_y=0$. We can represent the initial velocity using the initial angle:

\[\begin{split} v_{0x} = v_0 \cos \theta_0 \\ v_{0y} = v_0 \sin\theta_0 \\ \end{split}\]

$v_0 = |\vec{v_0}|$ is the magnitude (initial speed).

We can specify the velocity of a projectile as function of time:

\[\begin{split} x =x_0 + v_{0x}t \\ y = y_0 + y_{0y}t - \frac{1}{2}gt^2 \\ v_x = v_0 \cos \theta_0 \\ v_y = v_0 \sin \theta_0 - gt \end{split}\]

(If we start at the origin we can simplify $x_0 = y_0 = 0$) From this we can calculate the distance a projectile travels at any time:

\[ r = \sqrt{x^2 + y^2} \]

And the projectiles speed at any time: $$ v = \sqrt{u_x^2 + u_y^2} $$

And the angle at any time:

\[ \theta = \tan^{-1} \frac{u_y}{u_x} \]

Symmetry¶

The time that it takes to reach the highest point is the same as the time required to fall back.

study-notes

Projectile Motion¶

Symmetry¶