D-separation (Directed-Separation)¶
If we have 3 nodes A, B and C. Given the following structures we can derive independence assumptions
Common Parrent. Here \(A \leftarrow B \rightarrow C\) if we observer B then \(A \perp C | B\). If B contains all the information that determines the outcomes of A and C, than once we observe it there is nothing that affects these variable’s outcomes.
Cascade. Here if we observe B, than \(A \perp C | B\). \(A \rightarrow B \rightarrow C\) The inituition is that if B holds all the information that determines C, thus it does not matter what value A takes.
V-Structure \(A \rightarrow C \leftarrow A\). Here knowing C couples A and B, thus \(A \cancel{\perp} B | C\).
Probability view¶
We can look at these in terms of probabilities to make more sense:
\(X \rightarrow Y \rightarrow Z\)
Can be encoded as \(p(x,y,z) = p(x)p(y|x)p(z|y)\) when we condition on y are x and z independent?
\[ p(x,z|y) = \frac{p(x)p(y|x)p(z|y)}{p(y)} = \frac{p(x,y)p(z|y)}{p(y)} = p(x|y)p(z|y) \Rightarrow x \perp z | y \]\(X \leftarrow Y \rightarrow Z\)
\(p(x,y,z) = p(y)p(x|y)p(z|y)\) if we condition on y are x and z indepedent?
\[ p(x,z|y) = \frac{p(x,y,z)}{p(y)} = \frac{p(y)p(x|y)p(z|y)}{p(y)} = p(x|y)p(z|y) \Rightarrow x \perp z | y \]\(X \rightarrow Y \leftarrow Z\)
\(p(x,y,z) = p(x)p(z)p(y|x,z)\) if we condition on y are x and z indepenedent?
\[p(x,z|y) = \frac{p(x)p(z)p(y|x,z)}{p(y)} \Rightarrow x \cancel{\perp} z| y\]However \(p(x,z) = p(x)p(z)\), x and z are marginally independent. The condition on a common child at the bottom of a v-structure makes its parents become dependent. This effect is called explaining away, inter-causal reasoning, Berkson’s paradox.
An example would be 2 coins flips, they are iid, but if we would condition on their sum sudenly it provides us information about those flips.
Bayes Ball algorithm¶
We can visualize d-separation between \(X,Y,Z\), by conditioning on \(Y\) by shading it gray. If we bounce a ball from X or Z, where \(Y\) bounce it away, we look if it can reach any other node. A ball however can travel in an opposite direction.
\(X \rightarrow Y \rightarrow Z\)
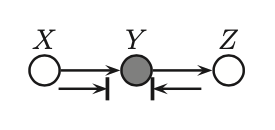
The ball bounces back.
\(X \leftarrow Y \rightarrow Z\)
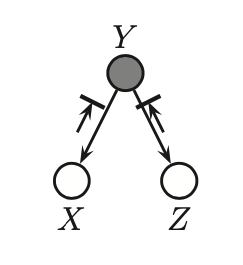
The ball bounces back.
\(X \rightarrow Y \leftarrow Z\)
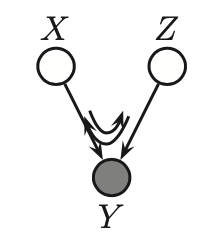
Here a ball bounces from X trough Y to Z. And vice versa. This makes intuitively sense, since X and Z are independent of each other. But if we know Y, that means that we can tell something about Z.
