Hierarchical adaptive lasso¶
Principal problems with lasso is that it results in biased estimates. This is because it needs to use a large value of \(\lambda\) to “squash” the irrelevant parameters, but this then over-penalizes the relevant parameters. It would be better if we could associate a different penalty parameter with each parameter.
\[\begin{split}
\gamma_j \sim IG(a, b) \\
\tau_j^2| \gamma_j \sim Gamma(1, \gamma_j^2/2) \\
w_j | \tau_j^2 \sim N(0, \tau_j^2)
\end{split}\]
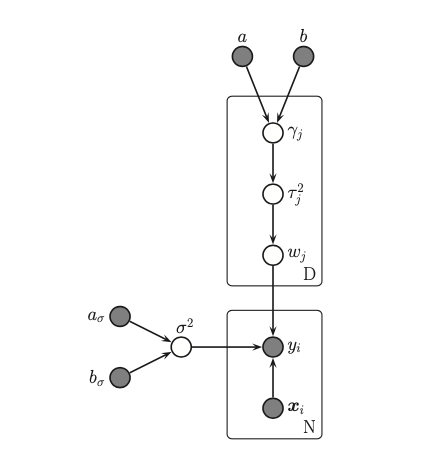
This model is known as hierarchical adaptive lasso. It yields an result that is much sparser than yielded by Lasso, but it is also less biased.
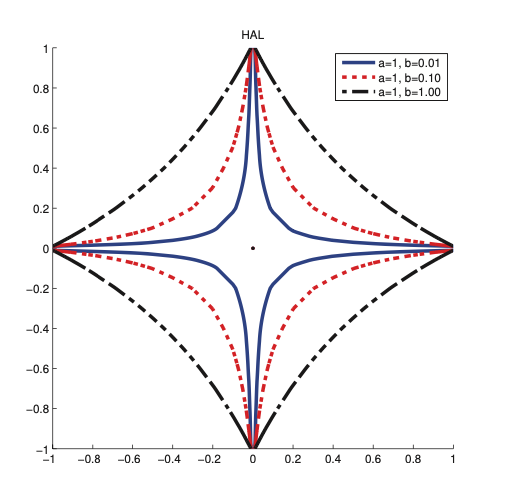
Compared to the diamond shaped Laplace penalty, the HAL penalty looks more like a starfish. Hence it puts more density on the spikes, thus enforcing sparsity more aggressively. This penalty is not convex.
