Contents

Chow Liu Algorithm¶

The Chow-Liu algorithm a score based approach to find structure in bayesian networks. The algorithm finds the maximum-likelihood tree (since we limit ourselves to trees only, we do not need to have additional penalty terms) structure where each node has at most one parent.

Algorithm¶

  1. Compute the mutual information for all pairs of variables X,U and form the mutual information graph where the edge between variable X, U has weight MI(X,U): $\( MI(X,U) = \sum_{x, u} = \hat{p}(x,u)\log [\frac{\tilde{p}(x,u)}{\tilde{p}(x)\tilde{p}(u)}] \)$

    • \(\tilde{p,u} = \frac{\text{count}(x,u)}{\# \text{data points}}\) is the empirical distribution This function measures how much information U provides about X.

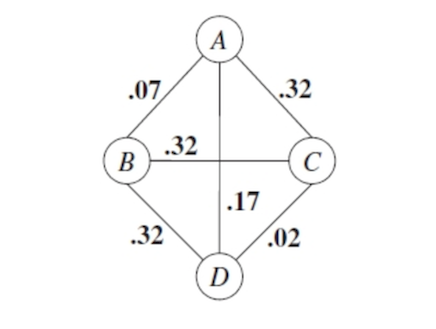
  2. Find the maximum weight spanning tree (Kruskal or Prim Algorithm)

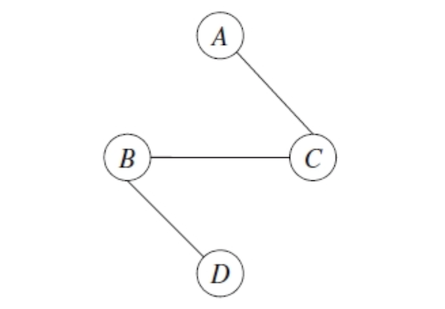
  3. Pick any node to be the root, and assign directions radiating outward from this node (arrows from it), we get a directed graph.

The complexity is \(O(n^2)\) to compute all the mutual information pairs, and \(O(n^2)\) to compute tha maximum spanning tree.

Why it works?¶

The likelihood score decomposes into mutual information and cross entropy terms:

\[ \log p(D|\theta^{\text{ML}}, G) = |D|\sum_i MI_{\tilde{p}}(X_i, X_{\text{pa}(i)}) - |D| \sum_{i}H_{\tilde{p}}(H_i) \]

The entropies are independent of the ordering in the tree, only the mutual information weights with the choice of G.

\[ \arg \max_G \log P(D|\theta^{\text{ML}}(G), G) = \argmax_G \sum_i MI(X_i, X_{\text{pa}(i)}) \]

If \(G=(V,E)\) is a tree where each node has at most one parent we get:

\[ \arg \max_{G:G \text{ is a tree}} \log P(D|\theta^{\text{ML}}(G),G) = \arg \max_{G:G \text{ is a tree}} \sum_{(i,j) \in E}MI(X_i,X_j) \]

Mutual information is symmetric thus the orientation play no role.

Multinomial Empirical Bayes