Contents

Sampling from standard distributions¶

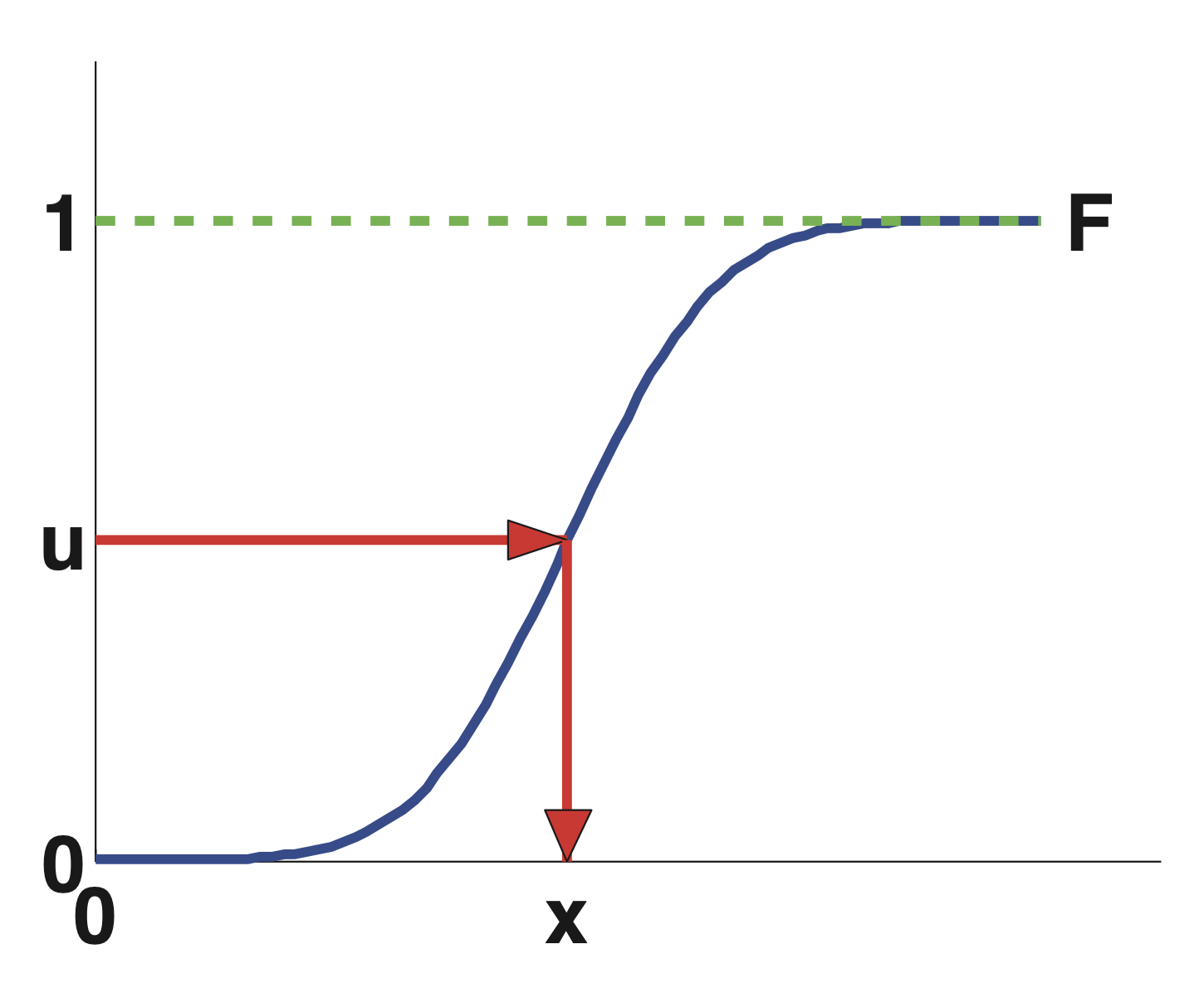
The siplest method to sample from an uniform distribution is based on the inverse probability transform. If \(F\) is the CDF then if we sample \(u \sim U(0,1)\) we can get a random variable by \(x = F^{-1}(u)\)

Sampling from a Gaussian¶

The main idea is that we sample from a unit radius circle, then we use the change of variables formula to derive samples from a spherical 2d Gaussian.

Sample \(z_1, z_2 \in (-1, 1)\), uniformly than discart that do not satistfy \(z_1^2 + z_2^2 \le 1\). These points will be uniformly distributed inisde the unit circle. Then we transform

\[x_i = z_i (\frac{-2 \ln r^2}{r^2})^{1/2}\]

for \(i = 1:2\) where \(r^2 = z_1^2 + z_2^2\). Using the multivariate change of variables formula we have:

\[ p(x_1, x_2) = p(z_1, z_2)| \frac{\partial (z_1, z_2)}{\partial (x_1, x_2)}| = [\frac{1}{\sqrt{2}\pi}\exp{(- \frac{1}{2} x^2_1)}][\frac{1}{\sqrt{2}\pi}\exp{(- \frac{1}{2} x^2_2)}] \]

Henc \(x_1\) and \(x_2\) are two independent samples form a univariate Gaussian This is known as the Box-Muller method

Elipse Map inference in graphical models