Linear Regression¶
We can define a regression model as follows:
\[p(y|x, \theta) = \mathcal{N}(y| w^Tx, \sigma^2)\]
We can generalize this to model non-linear relationships, by introducing a basis function \(\phi(x)\).
\[p(y|x, \theta) = \mathcal{N}(y| w^T\phi(x), \sigma^2)\]
This model is still linear in parameters. An example of a polynomial basis functions is:
\[\phi(x) = [1, x, x^2, \cdots, x^d]\]
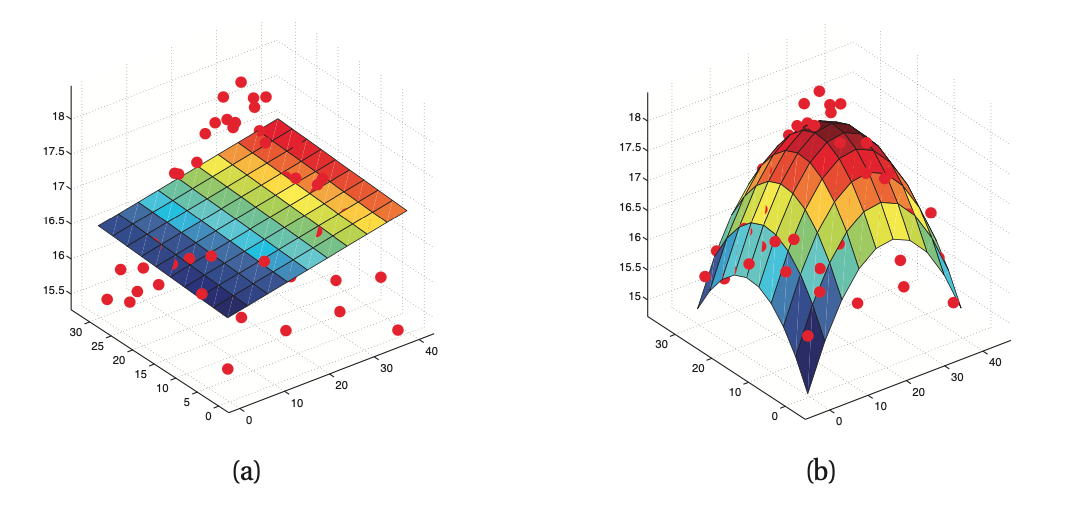
a) \(\hat{f}(x) = w_0 + w_1 x_1 + w_2x_2\)
b) \(\hat{f}(x) = w_0 + w_1 x_1 + w_2 x_2 + w_3x_1^2 + w_4 x_2^2\)
The later is a quadratic .
Fiting linear regression¶
The most common way is to perform ordinary least squares
