Principal Component as a Manifold¶

We can view probabilistic PCA as defining a thin pancake shaped region of high probability.

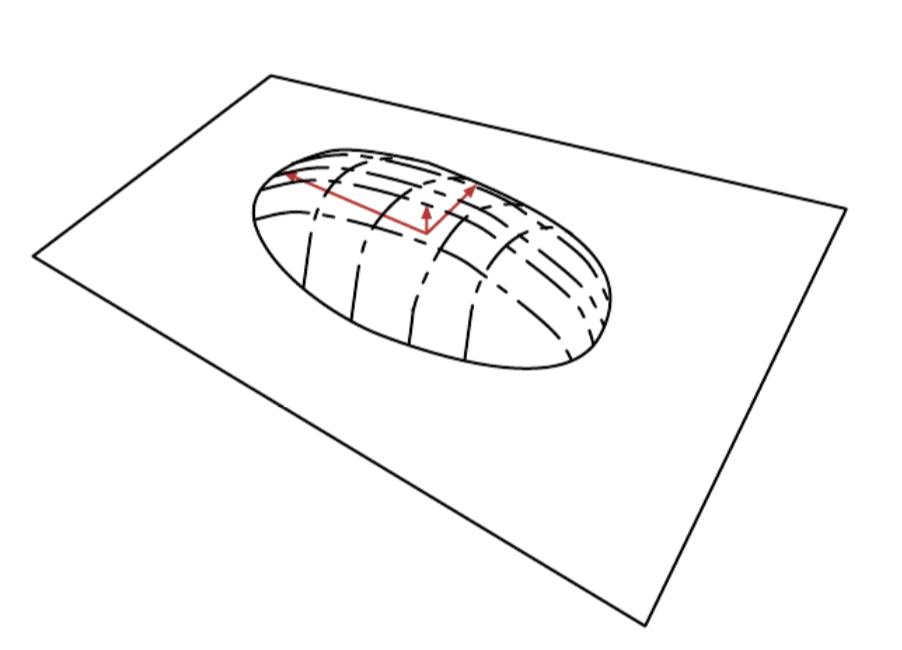
This is interpretation is valid for any linear autoencoder that learns matrices W and V with the goal of making the reconstruction of \(x\) lie as close to \(x\) as possible.

The encoder is:

\[ h=f(f) = W^T(x-\mu) \]

It computes an lower dimensional representation of \(h\). With the autoencoder we have also a decoder that reconstructs the input:

\[ \hat{x} = g(h) = b + Vh \]

The choice of linear encoder and decoder is to minimize the reconstruction error:

\[ E[||x - \hat{x}||^2] \]

With \(W=V, u,b = E[x]\) and \(W\) form an orthogonal basis, which spans the same subspace as the principal eigenvectors of the covariance matrix.

\[ C = E[(x-\mu)(x-\mu)^2] \]

For PCA the columns W are the eigenvectors ordered by the magnitude of the corresponding eigenvalues. We can show that the eigenvalue of \(x_i\) of \(C\) correspond to the variance of X in the direction of eigenvector \(v^{(i)}\). If \(x \in R^D\) and \(h\in R\) with \(d < D\) then the optimal reconstruction error:

\[ \min E[||x - \hat{x}||^2] = \sum_{i=d+1}^D \lambda_i \]

If the covariance has rand d, the eigenvalues \(\lambda_{d+1}\) to \(\lambda_D\) are 0 and the reconstruction error is \(0\).

The same solution can be obtained by maximizing the variance of the elements of \(h\), under orthogonal \(W\).

study-notes

Principal Component as a Manifold¶