Contents

Directed graphical models¶

Use directed graphs (DAG) to represent probability distributions.

Also known as

  • Bayesian network,

  • Belief networks, they representation is subjective.

  • Casual network, directed arrows model casual relationship

The key property of DAGs is that nodes can be ordered such that parents come before children. Given this ordering we define the ordered markov property, which assume that the children depend only on their parents, not on all the predecessors.

\[x_s \perp x_{preds(s) \ pa(s)} | x_{pa(s)} \]

  • preds(s) are the predecessors of the node s

  • pa(s) are the parents of node s

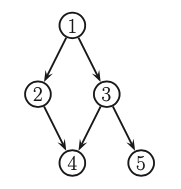
Now we can simplify the join distribution of the following graph

\[\begin{split} p(x_{1:5}) = p(x_1)p(x_2|x_1)p(x_3| x_1, \cancel{x_2})p(x_4| \cancel{x_1}, x_2, x_3) p(x_5, \cancel{x_1}, \cancel{x_2}, x_3, \cancel{x_4}) \\ = p(x_1)p(x_2|x_1)p(x_3|x_1)p(x_4|x_2, x_3)p(x_5|x_3) \end{split}\]

Formal definition¶

Bayesian Network is a directed graph \(G = (V,E)\) together with:

  • random variable \(x_i\) for each node \(i \in V\)

  • conditional probability distribution (CPD) \(p(x_i| x_{pa(t)})\) per node, specifying the probability of \(x_i\) conditioned on its parent’s values. (this is often defined as probability tables.)

It defines the following joint probability distribution. $\(p(x_{1:V}| G) = \prod_{t=1}^V p(x_i| x_{pa(t)})\)$

This probability distribution \(p\) defines an I-map (independence map).

If each node has \(O(F)\) parents and K states the number of parameters in the model is \(O(VK^F)\), which is much less than the \(O(K^V)\) needed by a model which makes no CI assumptions.

Examples¶

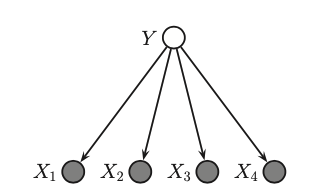
Naive Bayes¶

In naive bayes we assume that features are conditionally independent given the class label.

\[p(y,x) = p(y) \prod_{j=1}^D p(x_j|y)\]

Markov and hidden Markov Models¶

a) First order Markov chain, where the intermediate past \(x_{t-1}\) caputres everything wee need to know about the future.

b) Second order Markov chain and it corresponds to the folowing conditional distribution:

\[p(x_1,x_2) = \prod_{t=3}^T p(x_t| x_{t-1}, x_{t-2})\]

We can create higher order but then we need to have a lot of data.

c) Hidden Markov model (HMM) we assume that there is some hidden process that results in noisy observations.

Here \(z_t\) is known as hidden variable “at time t” and \(x_t\) is the observed variable. And the CPD \(p(z_t| z_{t-1})\) is the transition model and the CPD \(p(x_t|z_t)\) is the observation model.

The hidden variables represent quantities of interest, and in general we want to estimate the hidden state given the data, i.e to compute \(p(z_t|x_{1:t}, \theta)\). This process is called state estimation.

Learning¶

(2,4) Trees Back propagation