Functions of random variables¶
If \(X\) is a random variable than \(f(X)\) is also a random variable.
Since random variables are just mapings to the real line, than functions of random variables are just function \(f: R \rightarrow R\).
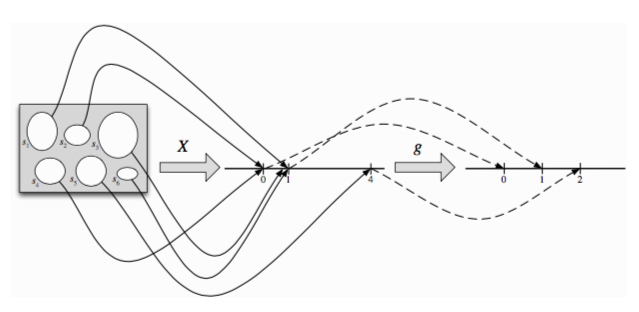
Linear functions¶
\[y = f(x) = Ax + b\]
We can derive the expectaion of \(y\):
Mean¶
\[ E[Y] = E[Ax + b] = A\mu + b \]
where:
\(\mu = E[X]\)
This is called the linearity of expectations
Variance¶
\[ var(Y) = var(Ax + b) = A \Sigma A^T \]
or in 1 dimension it is simply:
\[ var(y) = var(ax + b) = a^2 \sigma^2 \]
