Subgradient¶
Subgradients are generalization of gradients. Which is applicable for nondifferentiable functions.
Couple of facts:
For convex functions they allways exists
They may exists at points where functions are not differentiable
If a function is differentaible than the subgradient is just the gradient
Definition¶
For convex differentiable functions we have:
\(f(y) \ge f(x) + \nabla f(x)(y-x)\) for all \(x,y\) (This actually tells us that, if we approximate the function at any point using a linear approximation (\(f(x) + \nabla f(x)(y-x)\) intercept + slope), we always uderestimate the true value, except at x.
From this we define the subgradient, as a generalization of gradient, with the property:
Let \(g \in R^n\) be a subgradient of a convex function f at x such that:
\(f(y) \ge f(x) + g^T (y - x)\)
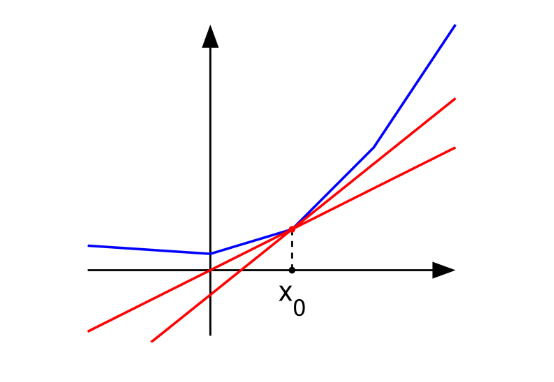
The red lines are subgradients. They allways underestimate.
