Contents

Wolfe Conditions¶

They relate to local descent and advise how to pick \(\alpha\) in:

\(f(x + \alpha d)\)

First Wolfe conditions¶

If \(d\) is a valid descent direction, then there exists a sufficiently small step size that satisfies the sufficient decrease condition.

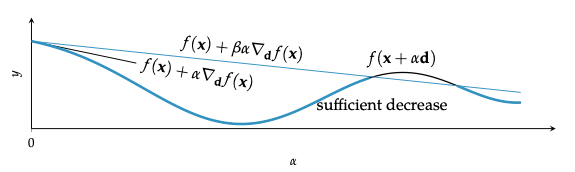
The first Wolfe condition is insufficient to guarantee convergence to a local minimum. Very small step sizes will satisfy the first condition but will prematurely converge.

Second Wolfe condition Curvature condition¶

Requires the directional derivative at the next iterate to be shallower:

\[ \nabla_{d^{(k)}} f(x^{(x+1)}) \ge \delta \nabla_{d^{(k)}} f(x^{(k)}) \]

\(\delta\) controls how shallow the next directional derivative must be. We commonly set it to be \(\beta < \delta < 1\). (For Conjugate gradient with approximate line search we set \(\delta = 0.1\), for Newtons method \(\delta = 0.9\))

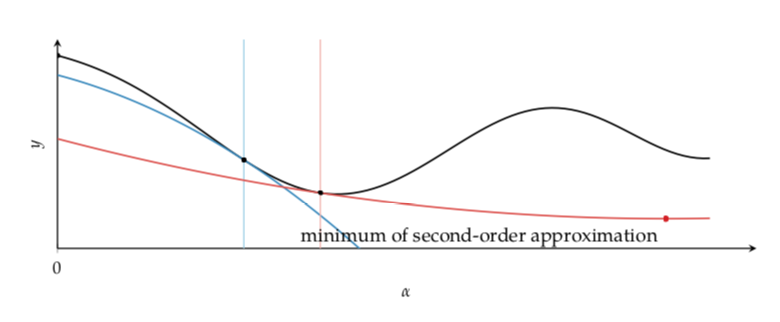The second Wolfe condition is necessary to ensure that the second order function approximation have positive curvature.

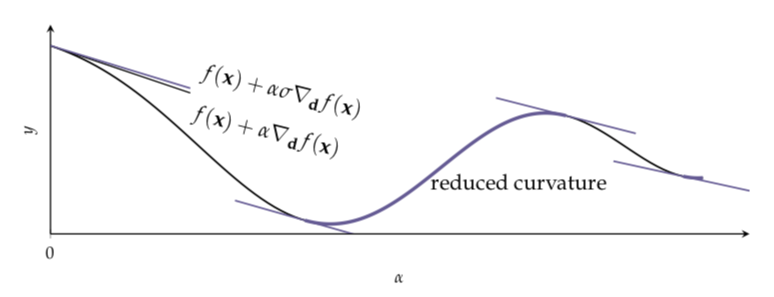Regions where the curvature condition is satisfied.

Strong Wolfe condition¶

An altenrative to the curvature conditions (more restrictive). It requires that the slope is not too positive:

\[ |\nabla_{d^k} f(x^{(k+1)})| \le - \delta \nabla_{d^k}f(x^{(k)}) \]

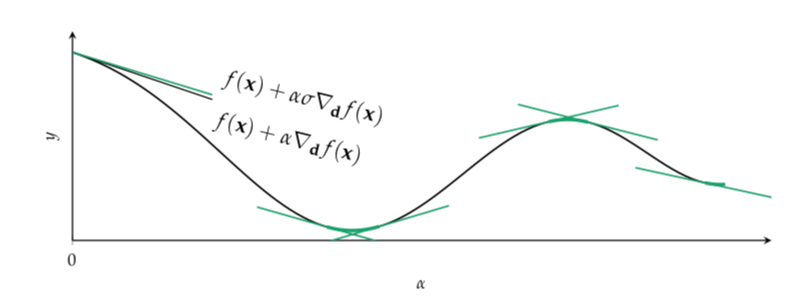
  • Together the sufficient decrease condition (First Wolfe) and the first curvature condition (Second Wolfe) form the Wolfe conditions.

  • The sufficient decrease condition with the second curvature condition form the strong Wolfe condition.

Batch and mini-batch algorithms Uniform circular motion