Contents

Hybrid discrete/continuous SSMs¶

Is a system that contians booth continuous and discrete hidden variables. A special case where we combine an HMM and LG-SSM we get switching linear dynamical system (SLDS), also called a jump Markov linear system (JMLS) or swithcing state space model (SSSM).

More precisely we have:

  • \(q_t \in \{ 1, 2, \cdots, K \}\) is a Discrete latent variable

  • \(z_t \in R^n\) is a Continuous latent variable

  • \(y_t \in R^D\) is the Continous observed random variable

  • \(u_t \in R^{U}\) is the optional Continous observed user input

Here we assume that the continous latent variables have a Linear Gaussian CPD conditional on the discrete state:

\[\begin{split} p(q_t=k|q_{t-1} = j, \theta) = A_{ij} \\ p(z_t| z_{t-1}, q_t = k, u_t, \theta) = \mathcal{N}(z_t| A_k z_{t-1} + B_k u_t, Q_t) \\ p(y_t| z_t, q_t = k, u_t, \theta) = \mathcal{N}(C_kz_t + D_k u_t, R_k)\end{split}\]

Where we can draw it as a graphical model:

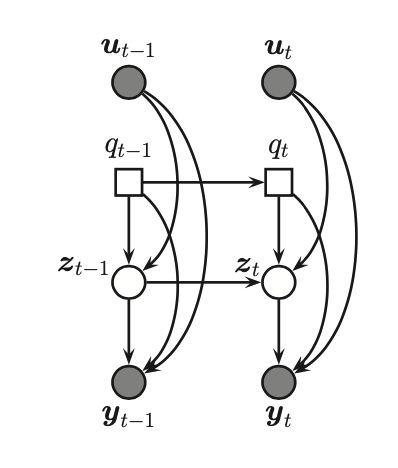
Inference¶

Unfortunately infrence in hybrid models, including switching LG-SSM model is intractable. Hence we need to use approximate inference methods:

  1. MC methods

Application¶

  1. Econometric forecasting

  2. Multi-target tracking

  3. Fault diagnosis

Metropolis Hastings mathematical formulation Basic trigonometry