Binary Tree¶
Binary tree is an ordered tree with the following properties:
Every node has at most two children
Each child node is labeled as being either a left child or a right child
A left child precedes a right child in the order of children of a node
Examples:
Answers to Yes-or-No questions (Decision tree).
An arithmetic expression can be parsed in this way.
We say a binary tree is proper if each node, except leaf nodes, has exactly 2 children. An nonempty proper binary three with \(n_E\) external nodes and \(n_I\) internal nodes holds \(n_E = n_i + 1\) (we can view the external node as a leaf).
Linked Structure for Binary Trees¶
In an linked structure each node stores an reference to its parent, to his left and right child and the element it contains. If a node does not have any children then the left and right references are None. Each tree contains the root element of the tree and also its size.
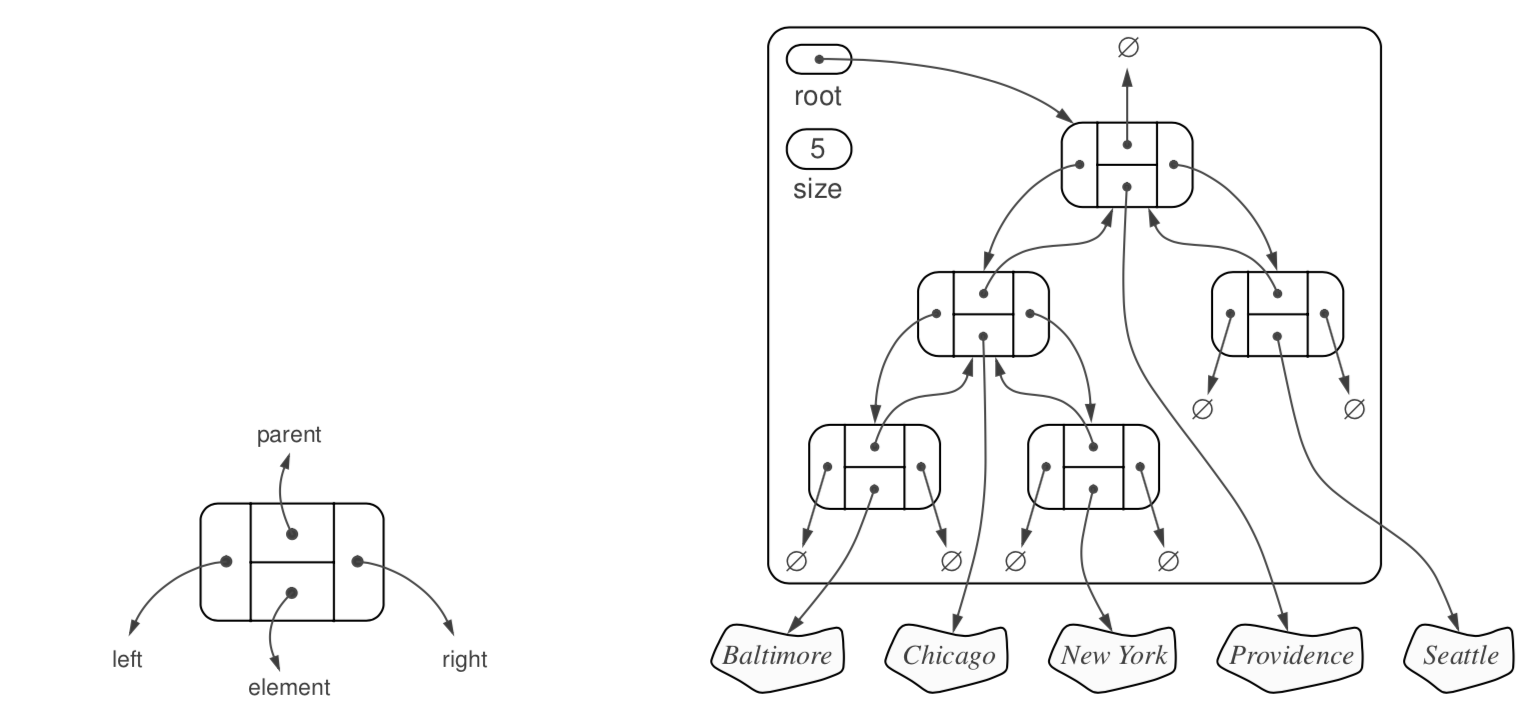
Array-Based Representation of Binary Trees:¶
We an number the positions of a binary tree T the following way:
If p is the root of T, then \(f(p) = 0\)
If p is the left child of position q, then \(f(p) = 2f(q) + 1\)
If p is the right child of position q, then \(f(p) = 2f(q) + 2\)
Here the function \(f\) is known as a level numbering of the positions in a binary tree T.
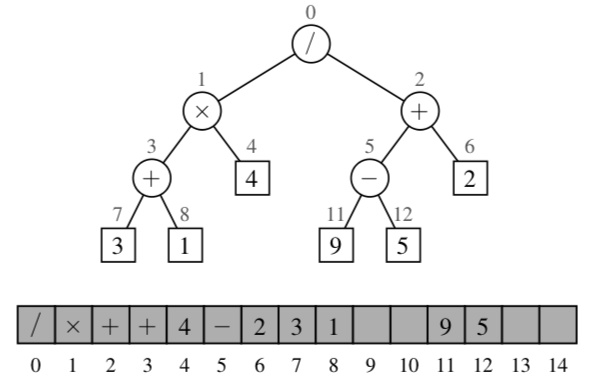
One advantage of an array-based representation of a binary tree is that a position p can be represented by a the single integer \(f(p)\) and position methods like root , parent, left, right can be implemented using simple arithmetic operations on the number f(p).
Here deletions are expensive we may copy a lot of nodes \(O(n)\)
