Multiway Search Tree¶
Let \(w\) be a node of an ordered tree, \(w\) is a d-node if it has \(d\) children. A multiway search tree to be an ordered tree T that has the following properties:
Each internal node of T has at least two children. That is, each internal node is a d-node such that \(d \ge 2\).
Each internal d-node w of T with children \(c_1, \cdots, c_d\) stores an ordered set of \(d-1\) key-value paris \((k_1, v_1), \cdots, (k_{d-1}, v_{d-1})\) where \((k_1, \le, \cdots, k_{d-1})\)
Let define \(k_0 = - \infty\) and \(k_d = + \infty\). For each item \((k,v)\) stored at a node in the subtree of w rooted at \(c_i, i = 1, \cdots, d\) we have that \(k_{i-1} \le k \le k_i\)
Thus any key k stored in a subtree of T rooted at a child node \(c_i\) must be between two keys stored at \(w\).
Example of an 2-4 search tree:
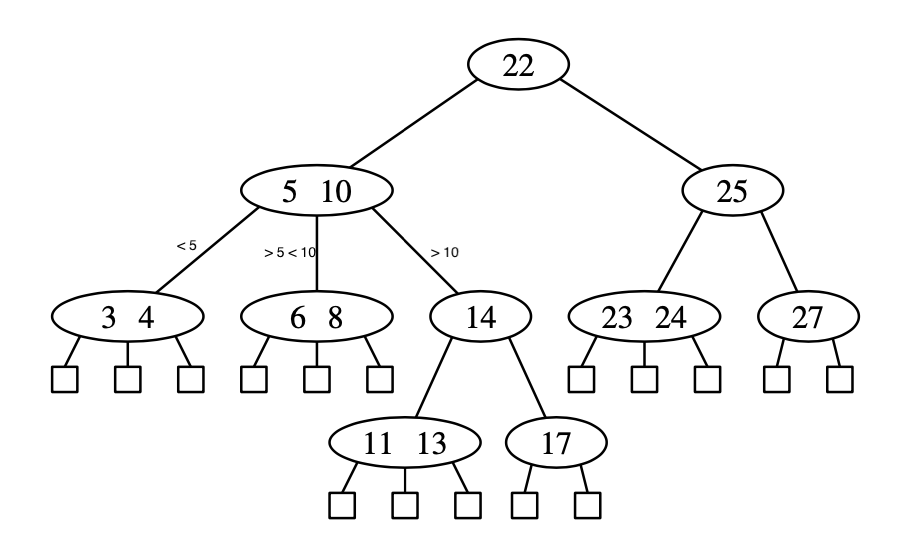
b) is a an unsuccessful search for 12, c) is the successful search path for 24
Searching in a Multiway Tree¶
We trace a path in T starting at the root. When we are at a d-node w during this search, we compare the key k with the keys \(k_1, \cdots, k_{d-1}\) stored at w. If \(k = k_i\) for some i, the search is successful. Otherwise we continue the search in the child \(c_i\) for w such that \(k_{i-1} < k < k_i\). If we search an external node we know that there is no item k in T.
Representing a Multiway Search Tree¶
At each node we have to store d-1 keys, during search we want to find the smallest key that is greater or equal to k. Thus we store the keys as SortedTableMap.
