Manifold learning¶
Manifold is a connected region. Mathematically it is a set of points associated with a neighborhood around each point. For any given point a manifold locally appears to be a Eucliedean space.
The concept of a neighborhood surround each point implies the existence of transformations that can be applied to movie a manifold form one position to a neighboring one. (World is an manifold we can walk north, south, west, east)
In ML we thing about a Manifold as a set of connected points that can be approximated well by considering a small number of degrees of freedom (dimensions) embedded in a high dimensional space. Each dimension corresponds to a local direction of variation.
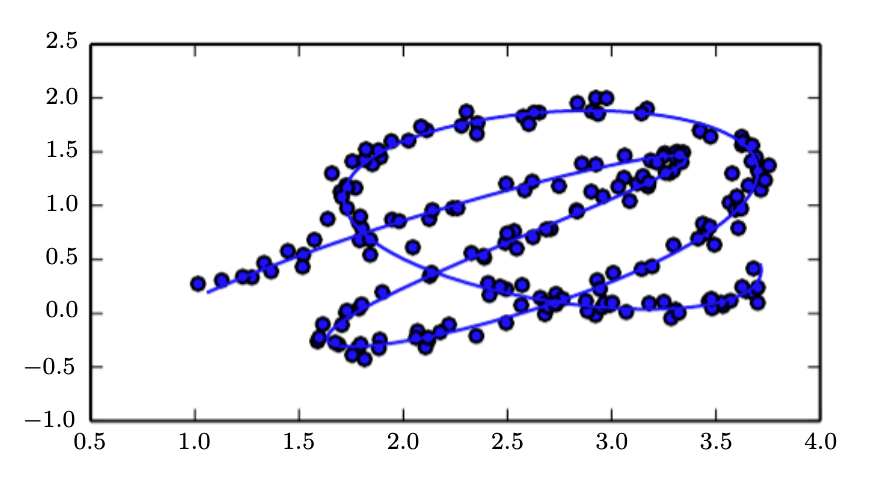
The solid line is the manifold we try to infer. It is a 2D space that is concentrated near a one-dimensional manifold like a twisted string
Most ML problems fail if we try to learn functions with interesting variations across all of \(R^n\). Manifold learning algorithms surmount this obstacle by assuming that most points in \(R^n\) are invalid, and interesting inputs happen along a collection of manifolds containing a small subset of points with interesting variations of the output learning function occurring only along directions that lie on the manifold or directions in which we move from one manifold to the other.
Manifold learning was introduces in real values unsupervised learning but this probability concentration can be generalized to discrete and (or) supervised settings. The key assumption is that the probability mass is highly concentrated.
For image, sound or text the manifold assumption is at least approximately correct with the following evidence:
probability distribution over images, text, sound that occur in real life is highly concentrated (a random set of pixel wont form an image nor random pick of letters)
we can imagine a neighborhood and transformations that allow us trace out a manifold over images (we can dim or brighten the lights or rotate the object)
