Rectified linear units (RELU)¶

It is an activation function used at hidden units of neural networks.

RELU is close to linear, because of this it preserves many of the properties that make linear functions easy to optimize. We can viewed it as a piece wise linear unit with two linear pieces.

\[ g(z) = \max(0, z) \]

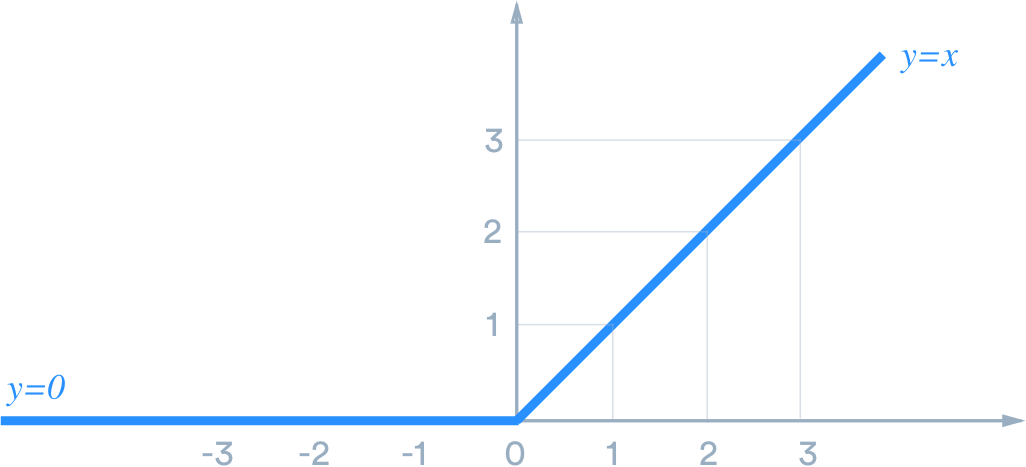
Cons¶

When \(z \le 0\) we cannot use gradient descent since the gradient is zero.

Generalized RELU¶

We generalize RELU to have gradient information everywhere. The basics idea is to define:

\[ h_i = g(z,\alpha)_i = \max(0, z_i) + \alpha_i \min(0,z_i) \space \text{ if } z_i < 0 \]

Absolute value RELU¶

We set \(\alpha_i = -1\) this yields:

\[ g(z) =|z| \]

This is useful in image recognition where we want features to be invariant under polarity reversal of the input illumination.

Leaky RELU¶

We set \(\alpha\) to a small value like 0.1

Parametric RELU¶

Here we try to learn the value of \(\alpha\)

Max out unit¶

This generalizes Relu by dividing z into groups of k values each unit outputting the max of its group:

\[ g(z)_i = \max_{j \in G^{(i)}} z_j \]

\(G^{(i)}\) set of indices one for each of the k groups

This can be viewed as the procedure of learning the activation function. If k is large enough we can approximate any convex function.

Each max out unit has \(k\) weight vectors instead of one, they require more regularization or more data. These multiple vectors serve as redundancy and can avoid catastrophic forgetting.

study-notes