Contents

PCA for categorical data

We can use this to visualize high dimensional categorical data.

\[\begin{split}p(z_i) = N(0,I) \\ p(y_i|z_i, \theta) = \prod_{r=1}^R \text{Cat}(y_{ir}|S (W^T_r z_i + w_{0r})) \end{split}\]

  • \(W_r \in R^{L \times M}\) is a loading matrix for response \(j\)

  • \(w_{or} \in R^M\) is offset term for response \(r\)

  • \(\theta = (W_r, w_{or})_{r=1}^R\)

  • \(\mu_0 = 0\) s the prior mean (we can capture non zero mean by changing \(w_{0j}\))

  • \(V_0 = I\) is the prior variance (we can capture non-identity covariance by changing \(W_r\))

Supervised PCA (Bayesian factor regression)

This is a model like PCA but it also takes the target variable \(y_i\) into account when learning the low dimensional embedding.

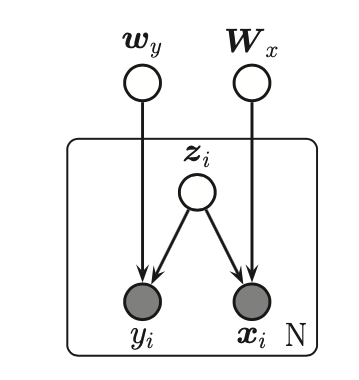
\[\begin{split}p(z_i) = N(0, I_L) \\ p(y_i|z_i) = N(w^T_y z_i + \mu_y, \sigma^2_y) \\ p(x_i| z_i) = N(w_x z_i + \mu_x, \sigma^2_x I_D) \end{split}\]

Since the model is jointly Gaussian we have:

\[y_i|x_i \sim N(x_i^Tw, \sigma^2_y + w_y^T Cw_y)\]

  • \(w = \Psi^{-1}W_xCw_y\)

  • \(\Psi = \sigma^2_x I_D\)

  • \(C^{-1} = I + W^T_x \Psi^{-1}W_x\)

Partial least squares

Is a more “discriminative” for of supervised PCA. The key idea is to allow some of the variance in the input features to be explained by its own subspace \(z_i^x\) and let the rest of the subspace \(z_i^s\) be shared between input and output.

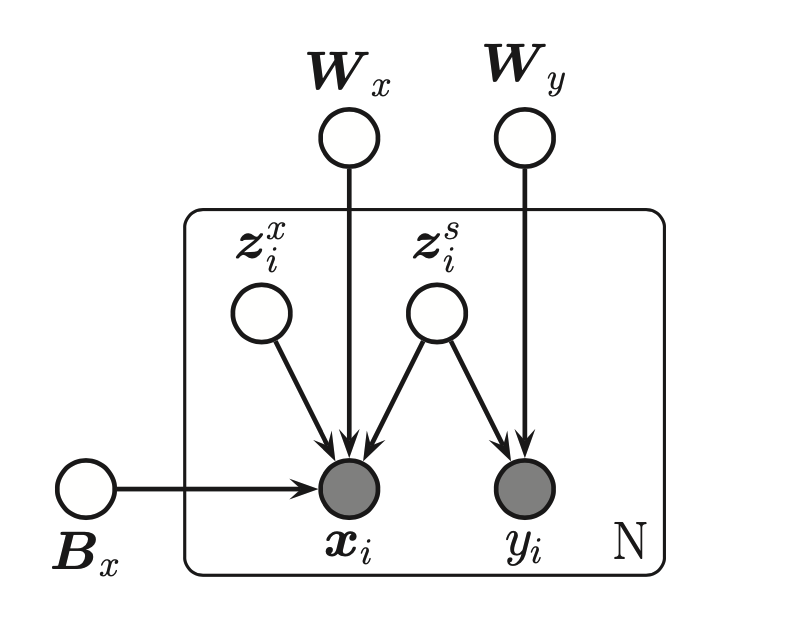
The model:

\[\begin{split} p(z_i) = N(z_i^s| 0, I_{L_s})N(z_i^x| 0, I_{L_x}) \\ p(y_i|z_i) = N(W_y z_i^s + \mu_y, \sigma^2 I_{D_y}) \\ p(x_i|z_i) = N(W_x z_i^s + B_x z_i^x + \mu_x, \sigma^2 I_{D_x}) \end{split}\]

The corresponding induced distribution on the visible variables has the form:

\[ p(v_i| \theta) = \int N(v_i| Wz_i + \mu, \sigma^2I) N(z_i|0, I)dz_i = N(v_i|\mu, WW^T + \sigma^2I)\]

  • \(v_i = (x_i ; y_i)\)

  • \(\mu = (\mu_y ; \mu_x)\)

And:

\[\begin{split} W = \begin{bmatrix} W_y & 0 \\ W_x & B_x \end{bmatrix} \end{split}\]

Canonical correlation analysis

Canonical correlation analysis or CCA is like a symmetric unsupervised version of Partial least squares. It allows each view to have its own “private” subspace, but there is also a shared subspace. If we have two observed variables \(x_i\) and \(y_i\) then we have three latent variables, \(z_i^s \in R^{L_0}\) wich is shared, \(z_i^x \in R^{L_0}\)and \(z_i^y \in R^{L_0}\) which are private. We can visualize the model as:

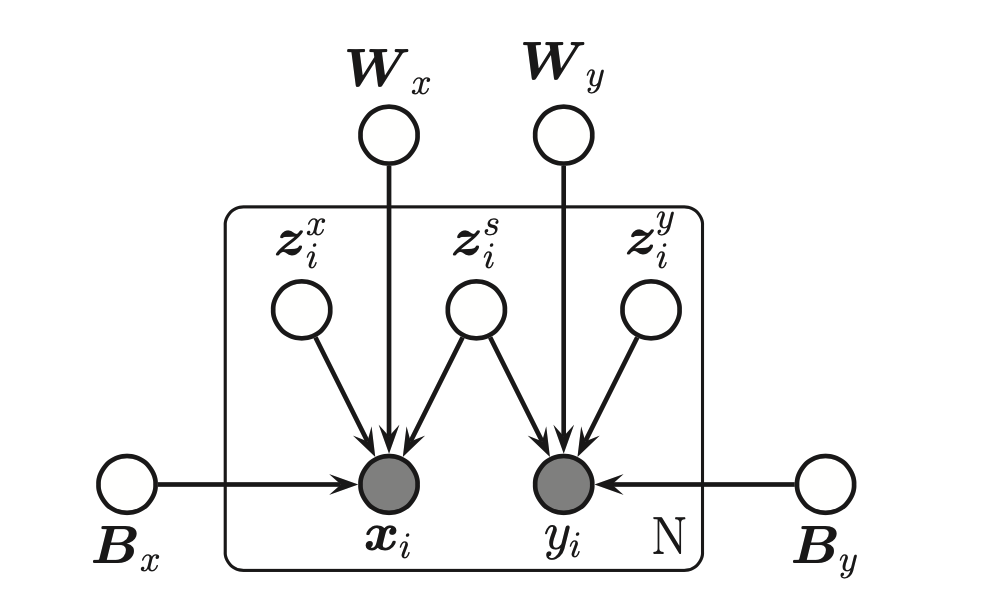
\[\begin{split} p(z_i) = N(z_i^s| 0, I_{L_s}) N(z_i^x|0, I_{L_s})N(z_i^y| 0, I_{L_y}) \\ p(x_i|z_i) = N(x_i| B_x z_i^x + W_x z_i^s + \mu_x, \sigma^2I_{D_x}) \\ p(y|z_i) = N(y_i | B_y z_i^y + W_y z_i^s + \mu_y, \sigma^2 I_{D_y}) \end{split}\]

The observed joint distribution has the form:

\[ p(v_i| \theta) = \int N(v_i| Wz_i + \mu, \sigma^2 I)N(z_i| 0, I) dzi = N(v_i| \mu, WW^T + \sigma I_D) \]

where

\[\begin{split} W = \begin{bmatrix} W_x & B_x & 0 \\ W_y & 0 & B_y \end{bmatrix} \end{split}\]
EM as variational inference Belief propagation