Contents

Optimality conditions for the lasso¶

The lasso objective has the form:

\[f(\theta) = RSS(\theta) + \lambda ||w||_1 \]

Unfortunatelly the \(l_1\) norm not differentiable. Because of this we have to use subgradients

For the function \(f(\theta) = |\theta|\) (absolute value) the subgradient is given by:

\[\begin{split} \nabla f(\theta) \begin{cases} {-1} & \text{ if } \theta < 0 \\ [-1, 1] & \text { if } \theta = 0 \\ {+1} & \text{ if } \theta > 0 \end{cases} \end{split}\]

To find the gradient we first differentiate \(RSS(\theta)\)

\[ \frac{\partial}{\partial w_j} RSS(W) = a_j w_j - c_j \]

  • \(a_j = 2\sum_i^n x^2_{ij}\)

  • \(w_{-j}\) is w without feature j

  • \(x_{i, -j}\) is the i th component of x without feature j

  • \(c_j = 2 \sum_i^n x_{ij} (y_i - w^T_{-j}x_{i, -j})\)

    • is the correlation between the \(j\) th feature \(x_{:,j}\) and the residual due the other features, \(r_{-j}= y - X_{:,-j} w_{-j}\).

    • magnitude of \(c_j\) is an indication of how relevant the feature j is.

If we add the subderivative to the penalty we get:

\[\begin{split} \nabla_{w_j}f(w) = (a_j w_j - c_j) + \lambda_{w_j} ||w||_j \\ = \begin{cases} \{ a_j w_j - c_j - \lambda \} & \text { if } w_j < 0 \\ [-c_j - \lambda, -c_j + \lambda] & \text { if } w_j = 0 \\ \{ a_j w_j - c_j + \lambda \} & \text{ if } w_j > 0 \end{cases} \\ \end{split}\]

Or:

\[\begin{split} X^T(Xw - y)_j \in \begin{cases} \{ - \lambda \} \text{ if } w_j < 0 \\ [-\lambda, \lambda] \text{ if } w_j = 0 \\ \{\lambda\} \text{ if } w_j > 0 \end{cases} \end{split}\]

Depending on the value of \(c_j\), the solution to \(\partial_{w_j} f(w) = 0\) can occur at 3 different values:

  1. \(c_j \le -\lambda\) the feature is strongly negatively correlated with the residual the subgradient is zero when \(w_j = \frac{c_j + \lambda}{a_j} < 0\)

  2. \(c_j \in [-\lambda, \lambda]\) feautre is weakly correlated with the residual the subradient is zero at \(\hat{w}_j = 0\)

  3. \(c_j > \lambda\) the feature is storngly correlated with the residual, subgradient is zero at \(\hat{w}_j = \frac{c_j - \lambda}{a_j} > 0\)

We can express \(w_j\) as:

\[\hat{w}_j = soft(\frac{c_j}{a_j}; \frac{\lambda}{a_j}) \]

This procedure is called soft thresholding:

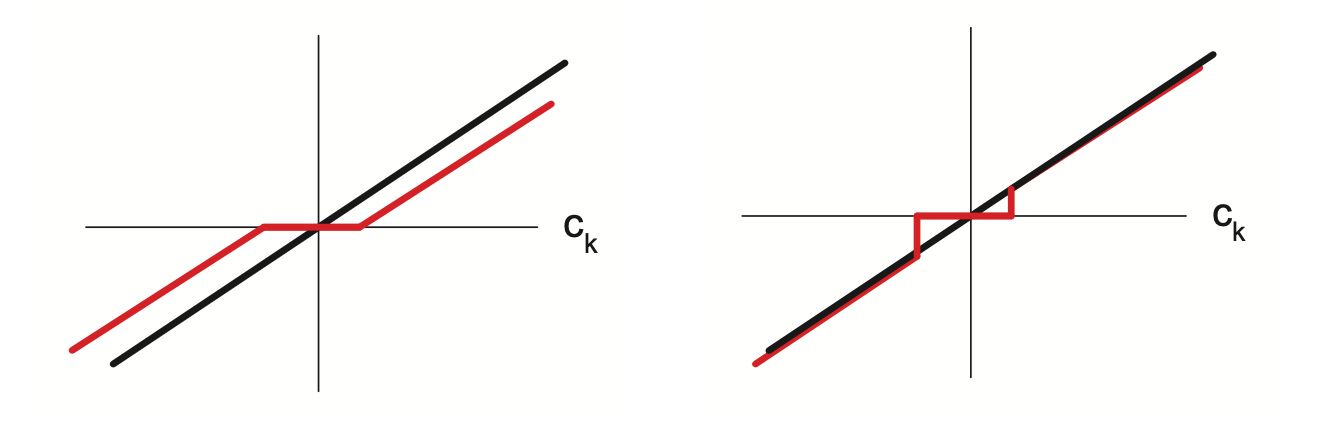
Here the bold black line prepresents the unregularized fit, and the red line the soft thresholded. In soft thresholding \(\hat{w}_j = 0\) if \(-\lambda \le c_j \le \lambda\). Also large values are shunken, and smaller are made larger, (lasso stands for least absolute selection and shrinkage operator) name) hence this makes lasso a biased estimator, since in general we do not want to shrink large values.

Maximal value of \(\lambda_{max}\)¶

\[ \lambda_{max} = ||X^Ty||_{\infty} = max_j |y^Tx_{:,j}|\]

If we set \(\lambda > \lambda_{max}\) we will get \(\hat{w} = 0\)

Hidden Markov models Exponential family