Variable elimination example¶
Lets look at the following Bayesian Network:
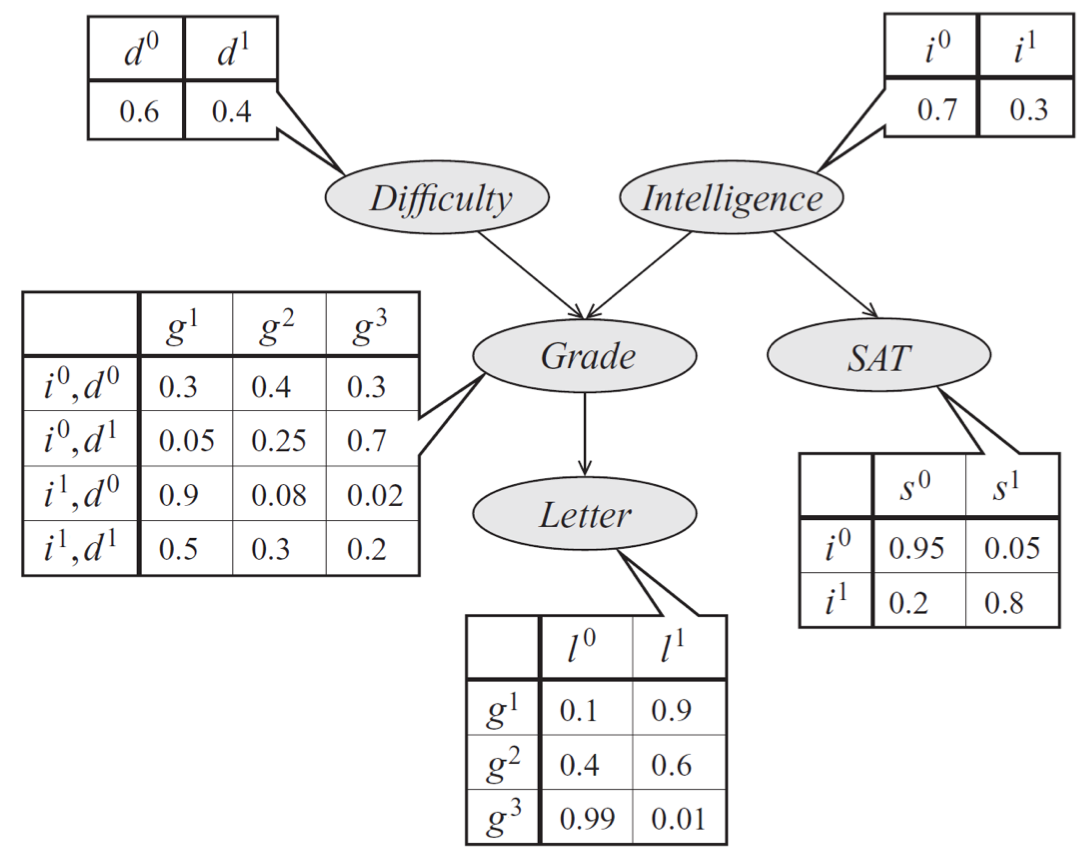
This model corresponds to the following distribution:
Our goal is to find \(p(l)\) by eliminating variables according to the topological ordering in the graph.
We going to eliminate in the order
At each step we create a factor: $\( \tau_1(g,i) = \sum_d p(g|i,d)p(d) \\ \tau_2(g,s) = \sum_i \tau_1(g,i)p(i)p(s|i) \\ \tau_3(g) = \sum_s\tau_2(g,s) \)$
The last step is to eliminate g, thus we get:
This takes up at most \(O(k^3)\)
If we would choose an different ordering it would be different. If we choose to eliminate \(g\) first we would have to transform the factors \(p(g|i,d)p(l|g)\) into \(\tau(d,il)\) this would require \(O(k^4)\) (k times for each conditional variable, and k times for each value of g). If we would have an factor \(p(g|s)\) we would require to eliminate it too and it would result in \(\tau(d,i,l,s)\) which would take \(O(k^5)\).
We can see that the ordering is making an large difference.
