Contents

Mixture of multinoullis¶

A mixture model where the data consists of D-dimensional bit vectors. The class conditional density is a product of Bernoullis

\[p(x_i|z_i = k, \theta) = \prod_{j=1}^D Ber(x_{ij}| \mu_{ij}) \]

  • \(\mu_{ij}\) is the probability that bit j turns on in cluster k.

The mean and covariance of this mixture model is given by:

\[ E[x] = \sum_x \pi_k \mu_k \]
\[ cov[x] = \sum_{k} \pi_k [\Sigma_i + \mu_k\mu_k^T] - E[x]E[x]^T \]

  • \(\Sigma_k = diag(\mu_{jk}(1 - \mu_{jk}))\)

Here the mixture distribution can capture correlations between variables.

Clustering¶

We can use a mixture model to create a generative classifier, where we model each class-conditional density \(p(x|y=c)\) by a mixture distribution.

We fit a mixture model, and compute \(p(z_i = k| x_i, \theta)\) which represetns the posterior robability that the point i belongs to cluster k. This is known as the responsibility of cluster k for point i and can be computed as:

\[r_{ik} \triangleq p(z_i = k| x_i, \theta) = \frac{p(z_i = k | \theta) p(x_i| z_i = k, \theta)}{ \sum_{k' = 1}^K p(z_i = k' | \theta) p(x_i| z_i = k', \theta) } \]

This is also known as soft clutering. We can transform it into hard clustering by using the MAP estimate by approximating

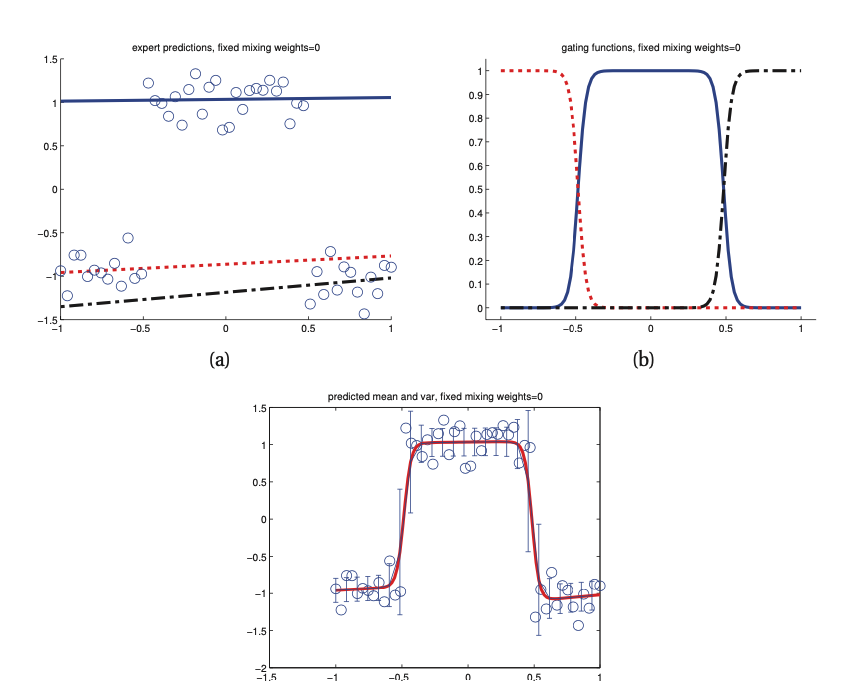
\[\hat{z_i} = \arg \max_k r_{ik} = \arg \max_k \log p(x_i | z_i = k , \theta) + \log p(z_i = k | \theta)\]

Mixtures of experts¶

We can use mixtures models for discriminative classification or regression. In this example we fit 3 different linear regression functions, each applying to different part of the input space.

\[\begin{split} p(y_i | x_i, z_i = k, \theta) = N(y_i| w^Tk x_i, \sigma^2_k) \\ p(z_i|x_i,\theta) = Cat(z_i | S(V^Tx_i)) \end{split}\]

This is called a mixture of experts.

Area and Volume Computing the marginal likelihood (evidence)