Law of total Probability¶
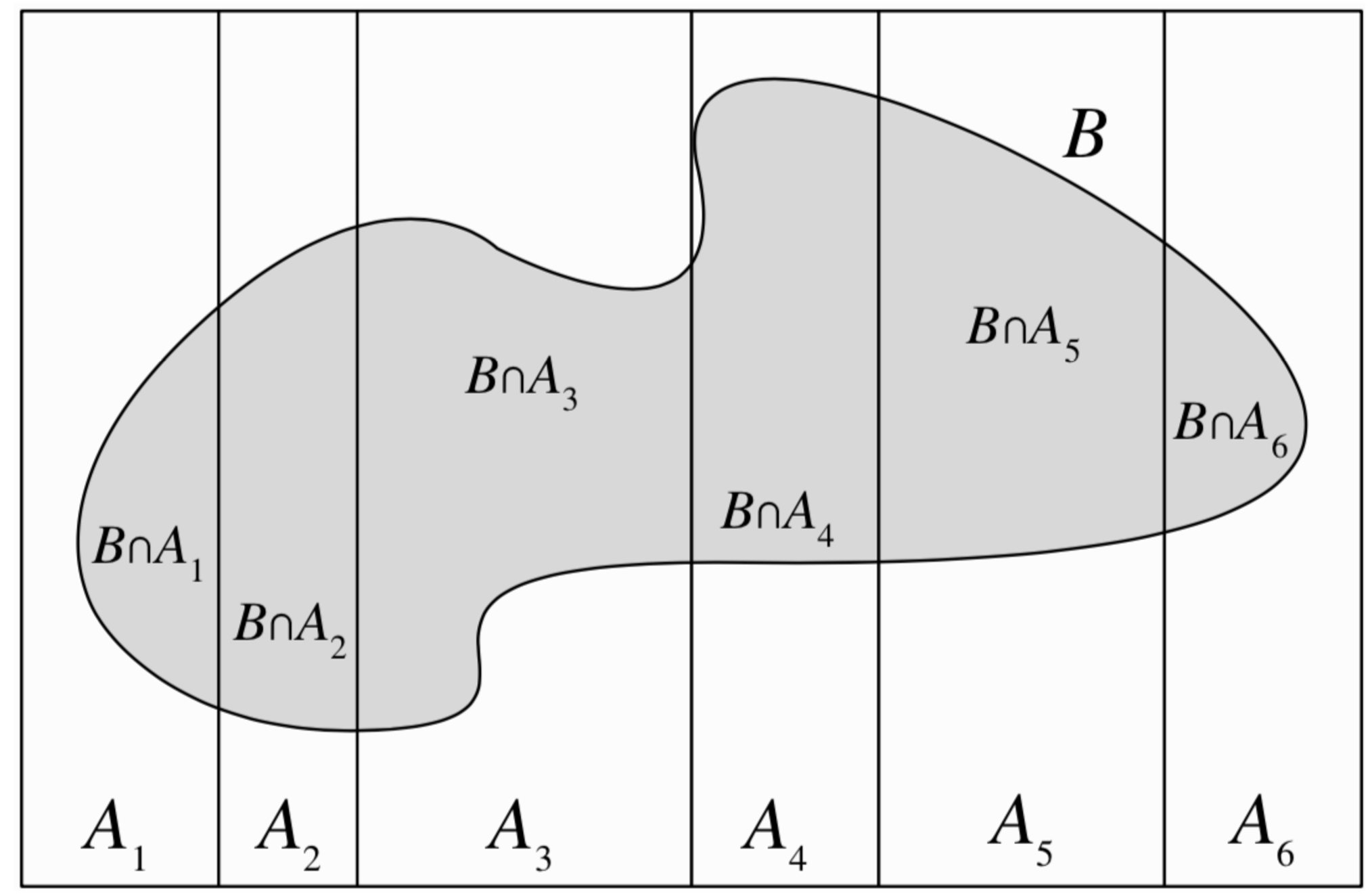
We define a partition \(A_1, A_2, \cdots, A_n\) on the sample space S, (\(A_i\) are disjoint and their union is S), with probability \(P(A_i) \ge 0\) for all i then:
\[P(B) = \sum_{i=1}^n P(B|A_i)P(A_i)\]
this comes from the fact that \(A_i\) form a partition on S, we can decompose B as:
\[B = (B \cap A_1) \cup (B \cap A_2) \cup \cdots \cup (B \cap A_n)\]
And visualy it looks as follows:
Conditional Law of total Probability¶
Let \(A_1, _2, \cdots, A_n\) for a partition on the sample space S. Provided that an event E has happend and \(P(A_i \cap E) > 0\) for all i we have $\(P(B|E) = \sum_{i=1}^n P(B|A_i,E)P(A_i|E)\)$
