Singular value decomposition (SVD)¶

Generalize eigen value decomposition for any matrix.

\[X = U S V^T\]

›

$X_{N \times D}$
$U_{N \times N}$ is orthonormal and is the eigen vectors of $XX^T$
$S_{N \times D}$ are the singular values where there is only $min(N,D)$ non zero.
$V_{D \times D}$is orthonormal and it is the eigne vectors of $X^TX$ (This is just the empirical covariance)

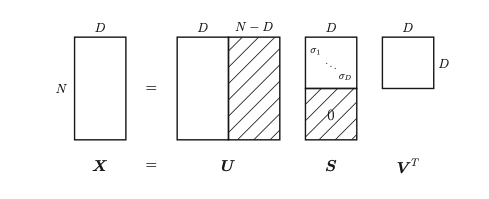
In general we do not need to compute all the columns of $U$ since they will be multiplied by zero. Thin SVD (Economy sized SVD) avoids computing those.

Connection between eigen vectors and singular values¶

Given a matrix $X = USV^T$ we have:

\[ X^TX = VS^TU^TUSV^T = V(S^TS)V^T = VDV^T \]

$D = S^2$ contains the square singular values

Hence $$ (X^TX) V = VD $$

That makes $V$ the eigen vectors of $X^TX$, the right singular vectors of X, and $D$ are its eigen values.

Similarly:

\[\begin{split} XX^T = USV^TVS^TU^T = U(SS^T)U^T \\ (XX^T)U = U(SS^T) = UD \end{split}\]

This makes $U$ the eigen vectors of U, and the left singular vectors of X

There is a special variant of SVD called truncated SVD which computes only the first L singular values. And gives the option to perform an rank L low rank approximation.

study-notes

Singular value decomposition (SVD)¶

Connection between eigen vectors and singular values¶