Red black trees¶

AVL trees may require many trinode restrucutre operations (rotations) to be performed after deletion, and 2-4 trees may require many split or fusing operations to be performed after an insertion or removal.

Red black trees use \(O(1)\) structural changes after an update in order to stay balanced.

An red-black tree is a binary search tree with nodes colored red and black in a way that satisfies the following properties:

Root Property the root is black
Red property The child of a red node are black
Depth property All nodes with zero or one children are the same black depth, defined as the number of black ancestors.

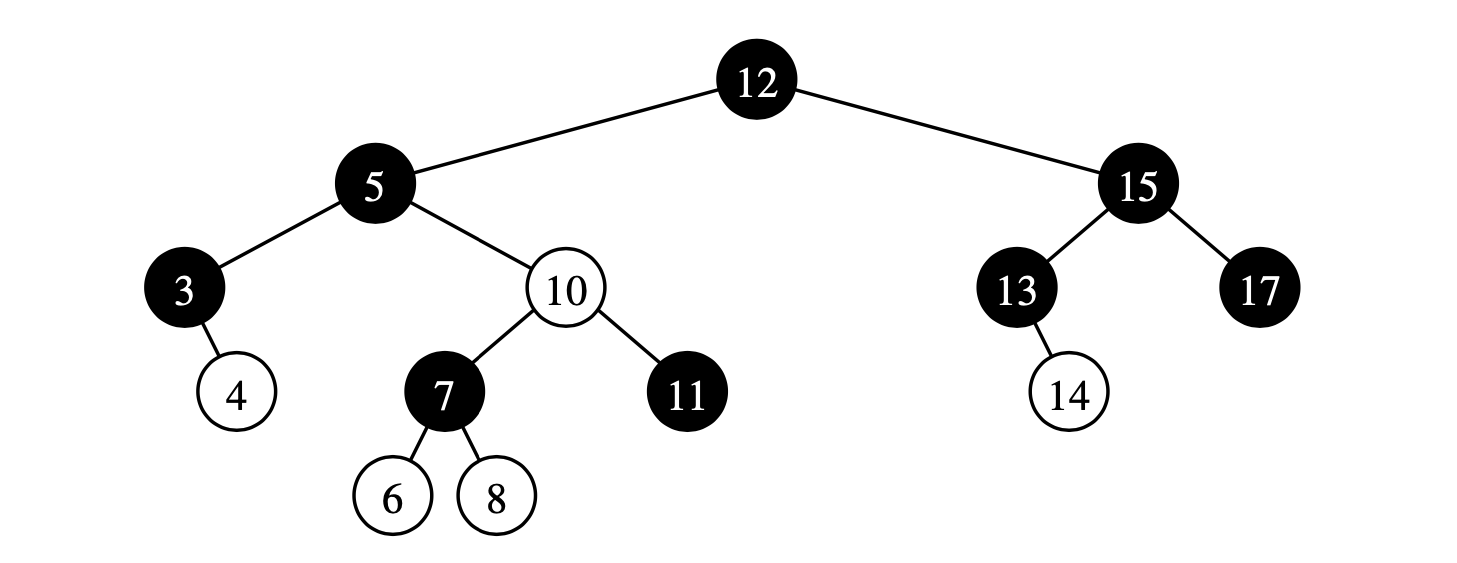
The height of a red-black tree storing n entries is \(O(\log n)\).

Connection to 2-4 trees ¶

There is an connection between 2-4 trees and red black trees.

Insertions¶

Insertion is the same as in a binary tree, we allways insert at a null subtree, and we introduce a new leaf x at this possition. If x the only node of T, thus is at the root we color it black. In all other cases we color x red. The insertions preserves the root and depth properties of T, but may violate the red property.

An example if x is not the root of T and the parent of y of x is red, then we have a parent and child (y and x) that are booth red. The root property is satisfied since y cannot be the root and be red, thus the parent z of y has to be black. Since x and its parent are red, but x’ grand parent z is black, this violation of red property is a double red at node x. To remedy we have to consider two cases:

The sibiling of s of y is Black (or None) To fix problem, we perform a trinode restructuring of T.
- Take node x, its parent y and grandparent z, relabel them a,b,c in left to right order, so that a,b and c will be visited in this order by an inorder tree traversal.
- Replace the grand parent z with the node labeled b, and make nodes a and c the children of b, keeping inorder relationship unchanged
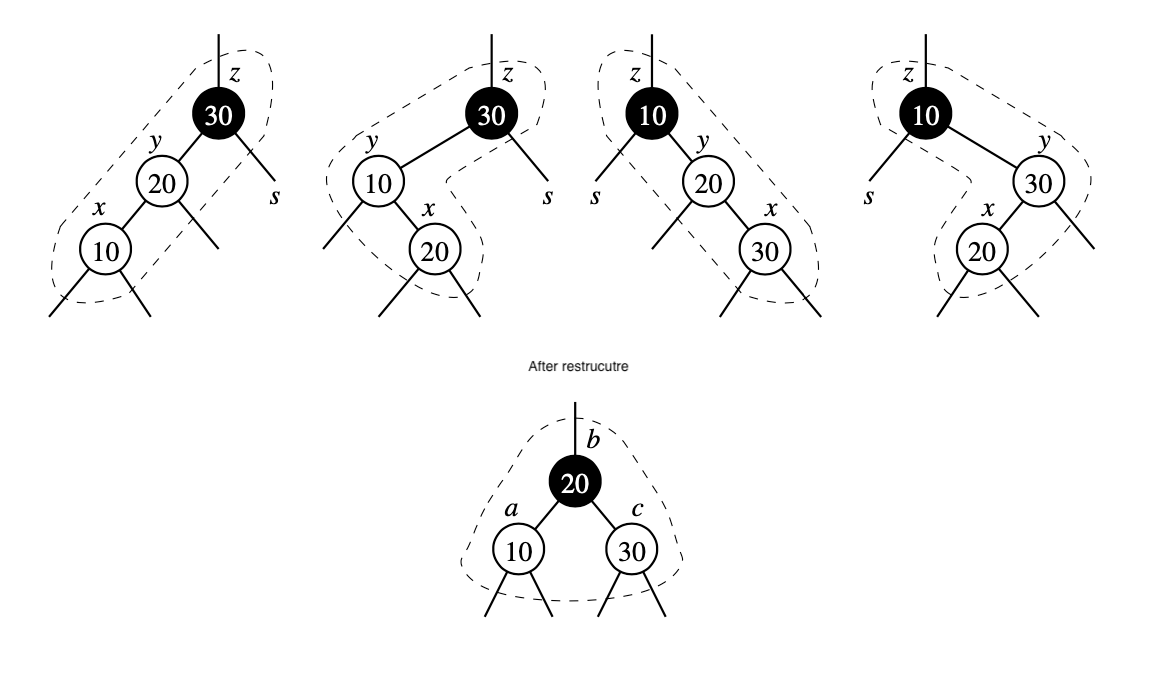
After restructure we color b black and we color a and c red.
The siblings s of y is Red

To fix this we do recoloring, we color y and s black and their parent z red (unless z is the root). Unless z is the root, the portion of any path trough the affected part of the tree is incident to exactly one black node, both before and after recoloring. Thus the black depth is unaffected after the recoloring. However, it is possible that the double-red problem reappears after such a recoloring higher up in the tree T, since z may have a red parent. If the double-red problem appears at z, then we repeat the consideration of the two cases at z. Thus a recoloring either eliminates the double red problem at node x, or propagates it to the grandparent z of x. We continue going up the tree until we finally resolve the double red-problem. The maximum number of recolorings cased by an insertions is no more than half the height of T.

recolor_2_4_tree

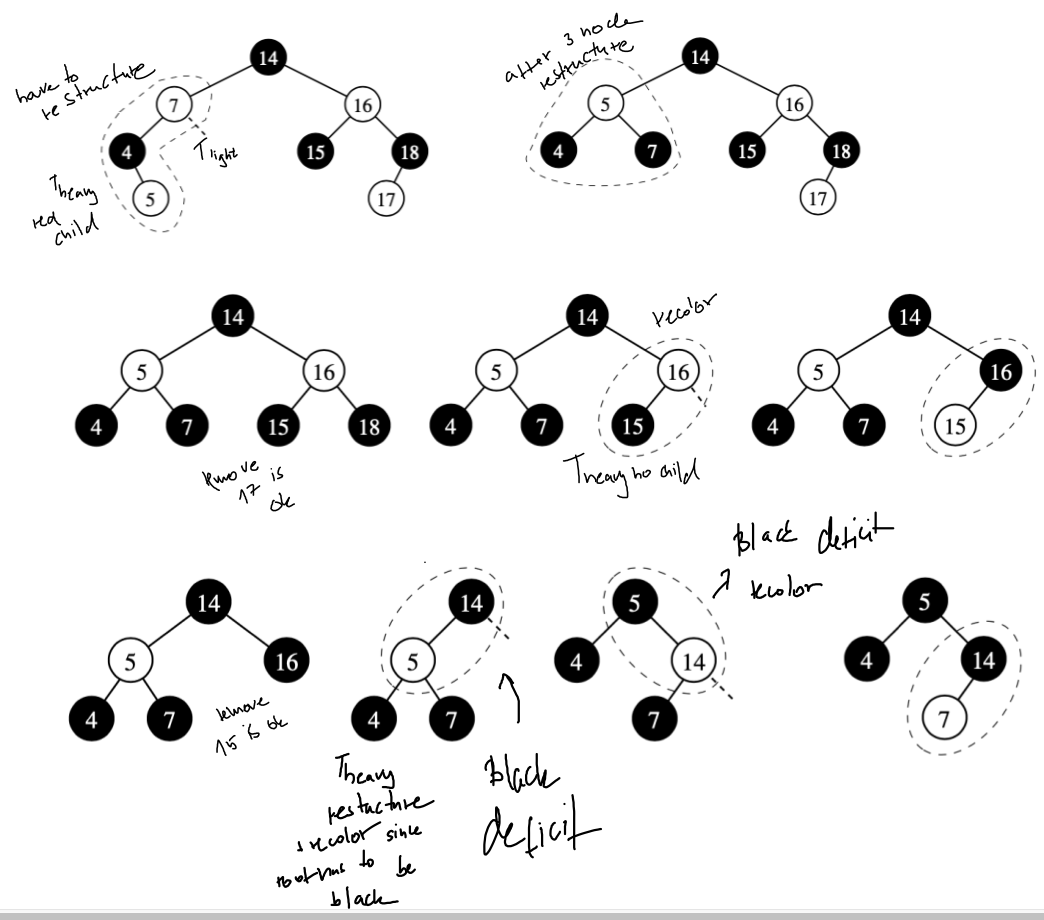
Example:

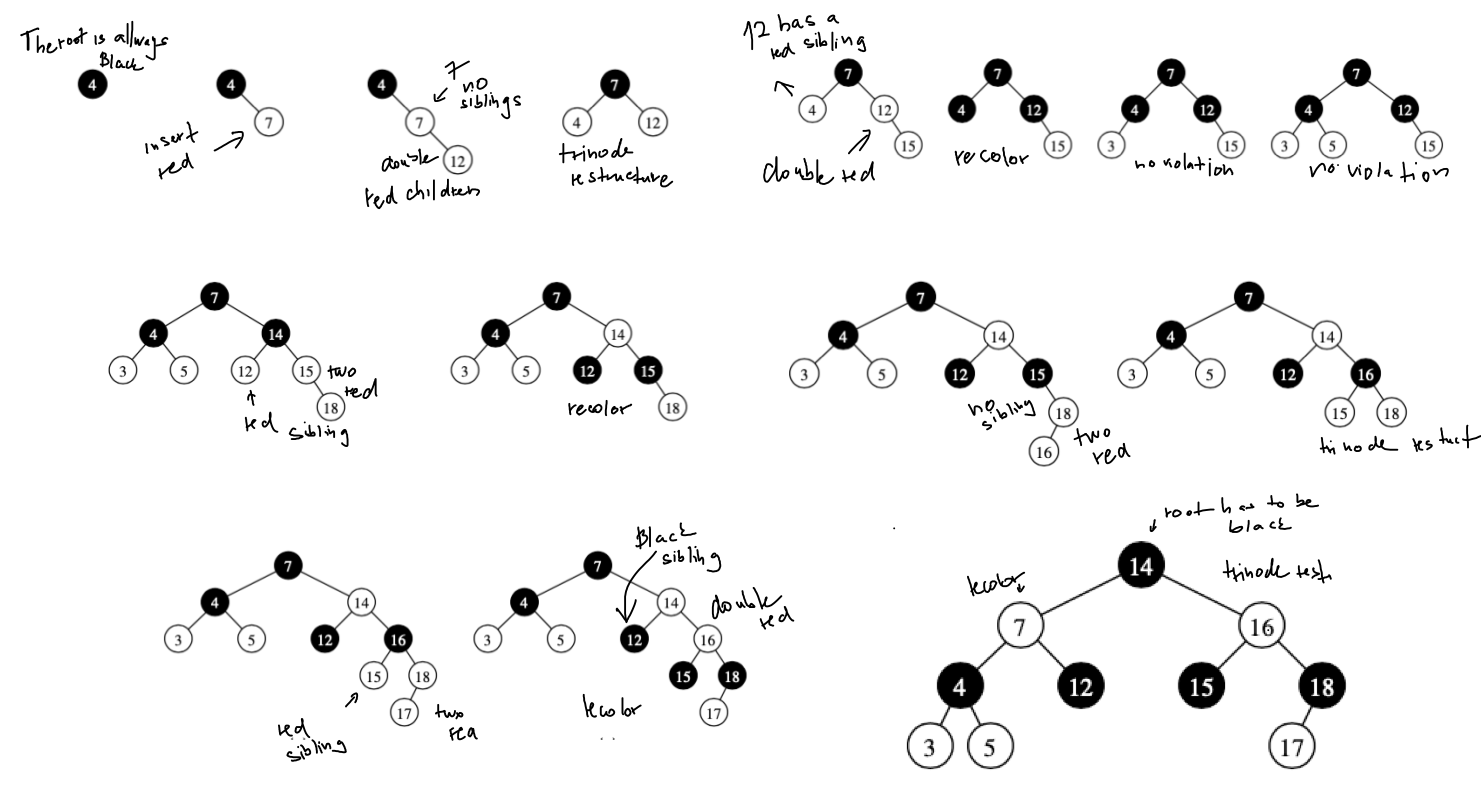
Deletion¶

We perform a binary search to find key k in T. Structurally the process results in the removal a node that has at most one child (either the one containing the key or its inorder predecesor) and the promotion of its remaining child (if any). If the removed node is red, it does not affect the black depths of any paths in the tree, nor introduce any red violations. If the removed node was black then it either had zero children or it had one child that was a red leaf. In the later case we restore the red-black property by recoloring the promoted child to black.

A more complex case is when a (nonroot) black leaf is removed. Without rebalancing, such a change results in a deficit of one for the black depth along the path leading to the deleted item. By necessity, the removed node must have a sibling whose subree has black height 1 (given that this was a valid red-black tree prior to the deletion of the black leaf). To remedy this, we consider a more general scenario with a node z, that is known to have two subrees, \(T_{\text{heavy}}\) and \(T_{\text{ligth}}\). The root of \(T_{\text{ligth}}\) is black and such that the black depth of \(T_{\text{heavy}}\) is exactly one more than that of \(T_{\text{light}}\).

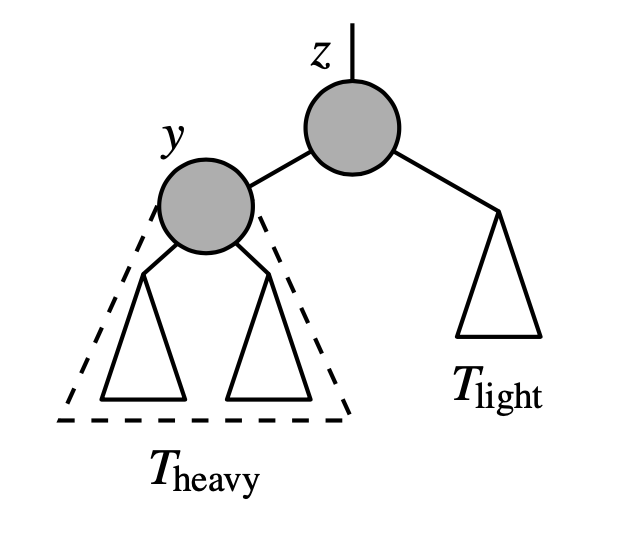
In this case a removed black leaf, z is the parent of that leaf and \(T_{\text{light}}\) is trivially the empty subree that remains after the deletion.

Node y is Black and Has a Red child x We perform a trinode restructuring, thus we take node x its parent y and grandparent z label them left to right a,b,c we replace z with the node labeled b making it the parent of two. We color a and c black ad give b the former color of z. In this case the path to \(T_{\text{light}}\) in the result includes one additional black node after the restrucutre, thereby resolving its deficit. In contrast the number of black nodes on paths to any of the other tree subrees remains unchanged.

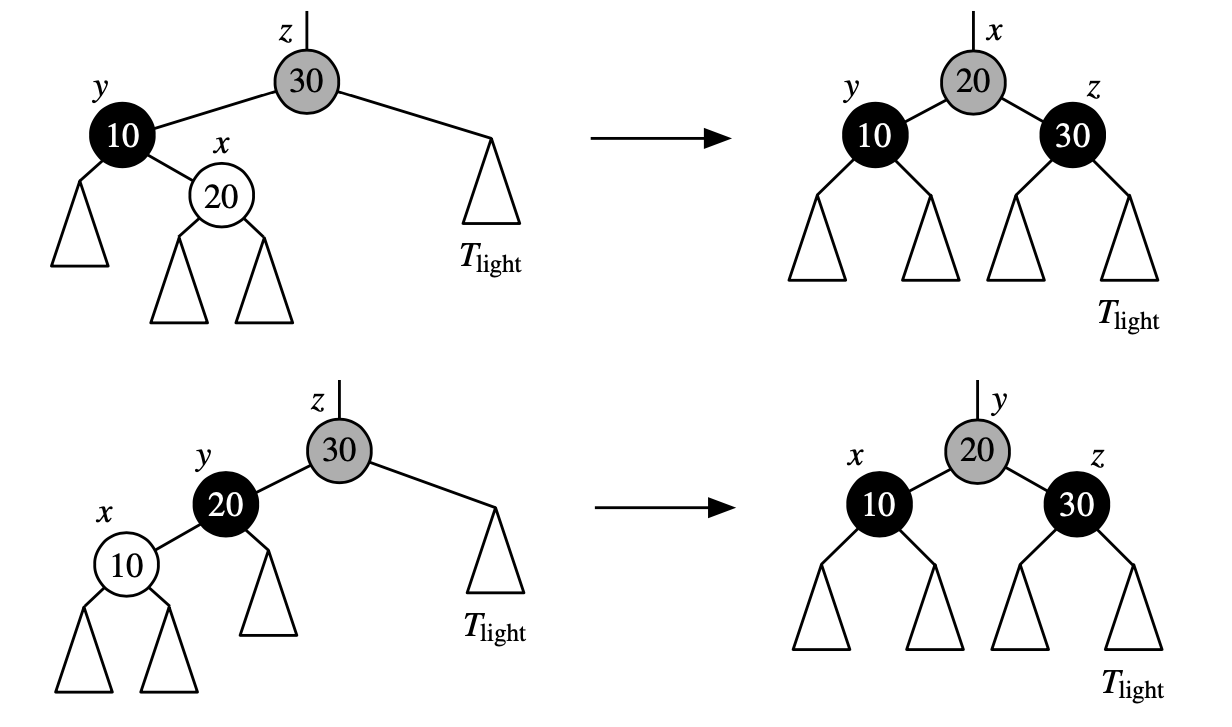This case corresponds to a transfer operation in the (2,4) tree T’ between two children of the node with z. Since y has a red child assures us that it represents either a 3-node or 4-node. In effect, the item previously stored at z is demoted to become a new 2-node to resolve the deficiency, while an item stored at y or its child is promoted to take the place of the item previosly stored at z.
Node y is Black and Booth children of y are Black (or None). We do a recoloring, we color y red and if z is red we color it black. This does not introduce any red-violations, because y does not have a red child. 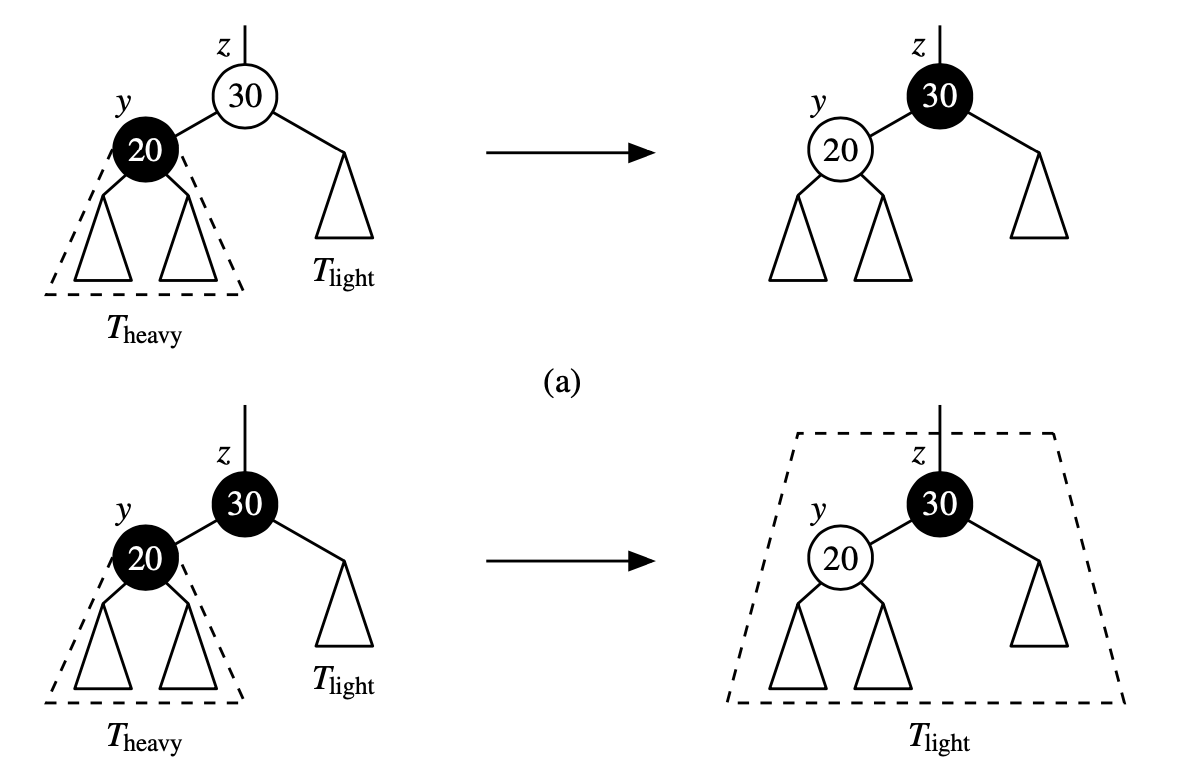Here we have 2 cases:

a) z is originally red, reversing the colors of y and z resolves the black deficit in \(T_{\text{light}}\) b) z is originally black, recoloring y cases the entire subtree z to have a black deficit requiring a cascading remedy.
Node y is Red Since y is red and \(T_{\text{heavy}}\) has black depth at least 1, z must be black and the two subtree of y must each have a black root adn a black depth equal to that of \(T_{\text{heavy}}\). In this case we perform a rotation about y and z, and then recolor y black ad z red.

This won’t immediately resolve the deficit, because z is an old subtree of y with black root \(y'\) and black height equal to that of the original \(T_{\text{heavy}}\). We reapply the algorithm to resolve the deficit at z, knowing that the new child \(y'\), that is the root of \(T_{\text{heavy}}\) is now black, and we can apply either Case 1 or Case 2.

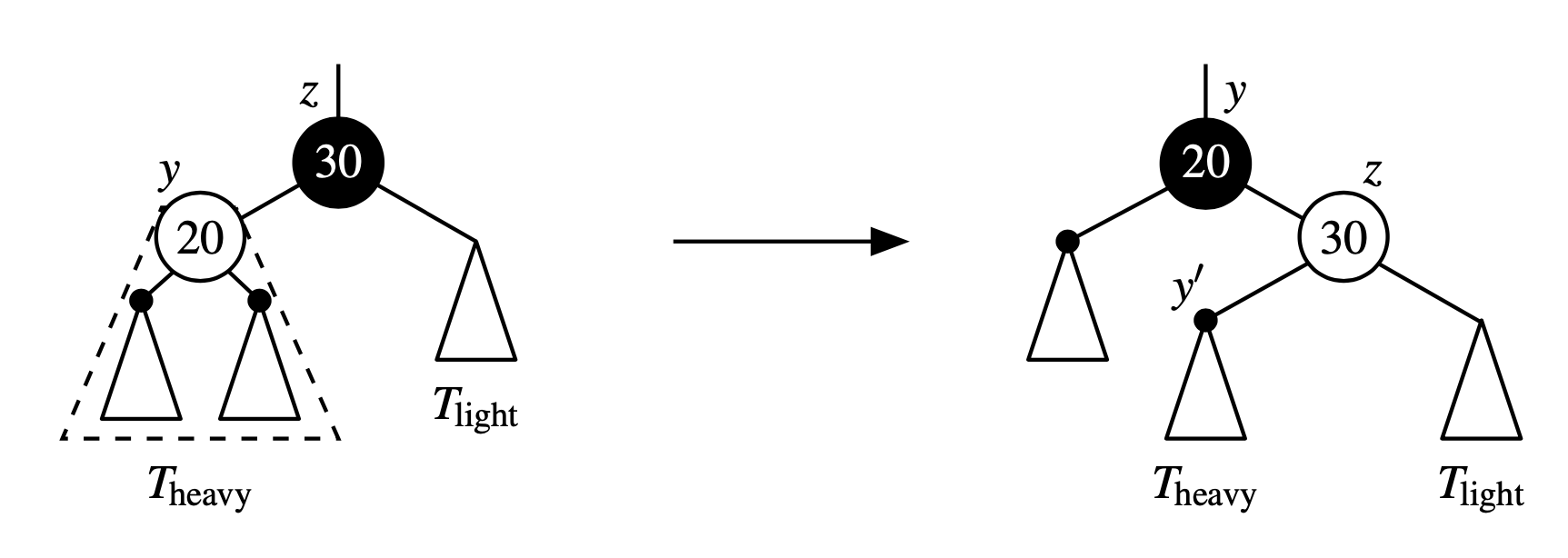A rotation and recoloring about red node y and black node z,assuming a black deﬁcit at z. This operation does not affect the black depth of any paths through this portion of the tree. Furthermore, because y was originally red, the new subtree of z must have a black root y′ and must have black height equal to the original \(T_{\text{heavy}}\). Therefore, a black deﬁcit remains at node z after the transformation.

Performance¶

The asymptotical performance is identical to AVL tree or (2,4) tree. The primary advantage of a red-black tree is that an insertion or deletion requires only a constant number of restructuring operations. Where AVL and (2,4) require a logarithmic number of structural changes per map operation in the worst case).

Insertion proposition¶

Insertions of an item in a a red-black tree storing n items can be done in \(O(\log n)\) time and requires \(O(\log n)\) recolorings and at most one trinode restructuring.

Deletion preposition¶

Deleting an item from a red black tree with n items takes \(O(\log n)\) time and performs \(O(\log n)\) recolorings and at most two restructuring operations.

study-notes