Plate notation¶
If we assume that the data is iid. There is a more compact representation for data.
The equation: $\(p(\theta|D) = p(\theta) [\prod_{i=1}^N p(x_i|\theta)]\)$
Can be expressed as:
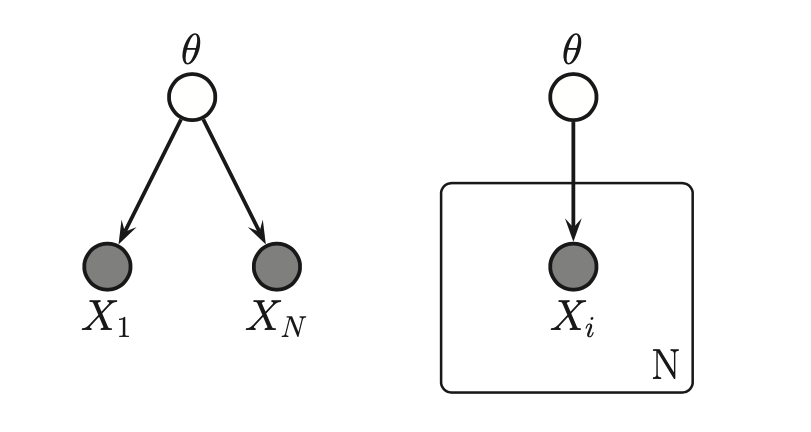
The picture with a plate represents that the total number of \(X_i\) is N. And it can be expanded as on the left. Here we assume that the data is conditionally independent only on the parameters \(\theta\), and it does not matter in which the data arrives. We say the data is exchangeable.
A plate is a little box around the repeated variables, and the convention is that nodes within the box will get repeated when the model is unrolled. The number of copies or repetitions is written in the bottom right corner of the box.
An more complex example:
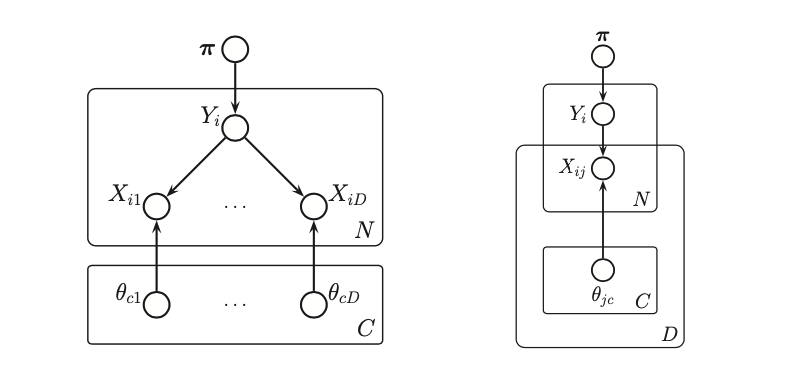
On the left we show a naive Bayes classifier that has been “unrolled” for \(D\) features, but uses a plate to represent repetition over cases \(i = 1 : N\). The version on the right shows the same model using nested plate notation. When a variable is inside two plates, it will have two sub-indices. For example, we write \(\theta_{jc}\) to represent the parameter for feature \(j\) in class-conditional density \(c\). What is not clear is that \(\theta_{jc}\) is used to generate \(x_{ij}\) iff \(y_i = c\) otherwise ignored. This is an example of context specific independence since the CI relationship \(x_{ij} \perp \theta_{jc}\) hold if \(y_i \ne c\)
