Random Variables¶
Is a variable that can take different values randomly. It is coupled with a probability distribution that specifies how likely each of the states are.
Alternatively we can view a random variable as a mapping from the sample space to the real line.
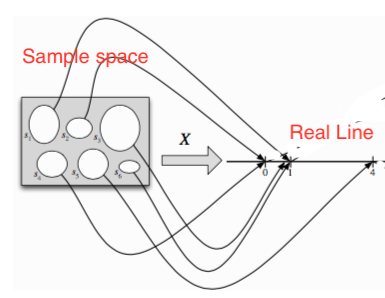
Mathematically speaking it is a function \(X: \Omega \rightarrow R\)
Discrete random variables¶
Is a random variable that can take up any value from a finite or countably infinite set X.
Continous random variables¶
Here X is infinite. Where we can express the probability that a random variable will be between \(a < b\) using the CDF:
\[
P(a < X \le b) = F(b) - F(a)
\]
