Recurrent neural networks conditioned on context¶
In most cases recurrent neural network are not just sequences of random variables \(y^{(t)}\) but also include inputs \(x^{(1)}, \cdots, x^{(t)}\). Because of this full conditional distribution is of the form:
\[
p(y|\theta(x))
\]
The common way to provide extra input are:
extra input at each time step
as the initial state \(h^{(0)}\)
boot above
Extra input at timestep¶
The whole vector from the beginning
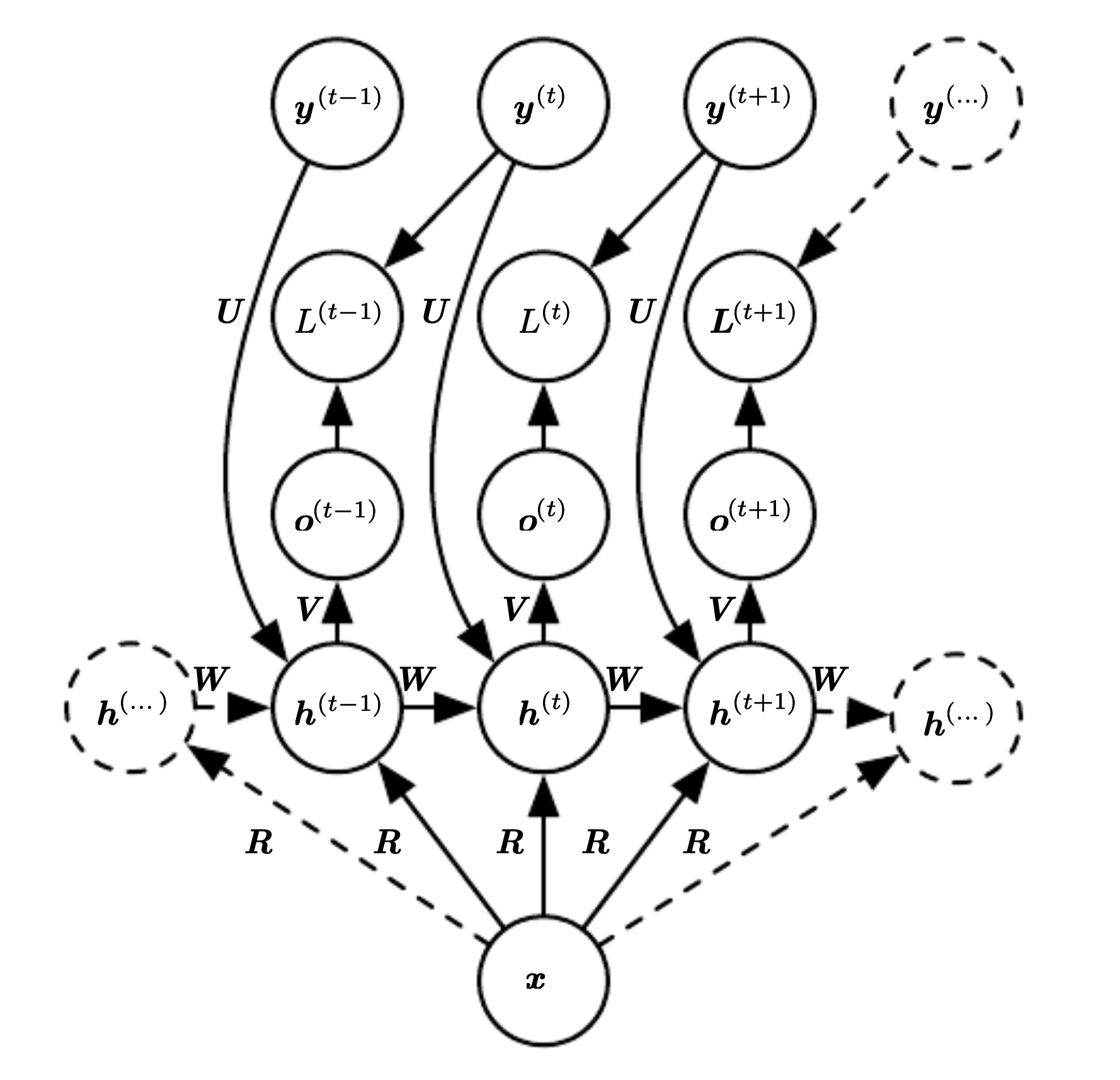
There is a single vector \(x=(x^{(1)}, \cdots, x^{(t)})\). We map the input using a weight matrix R and it is available at every step.
Only x^i at step i
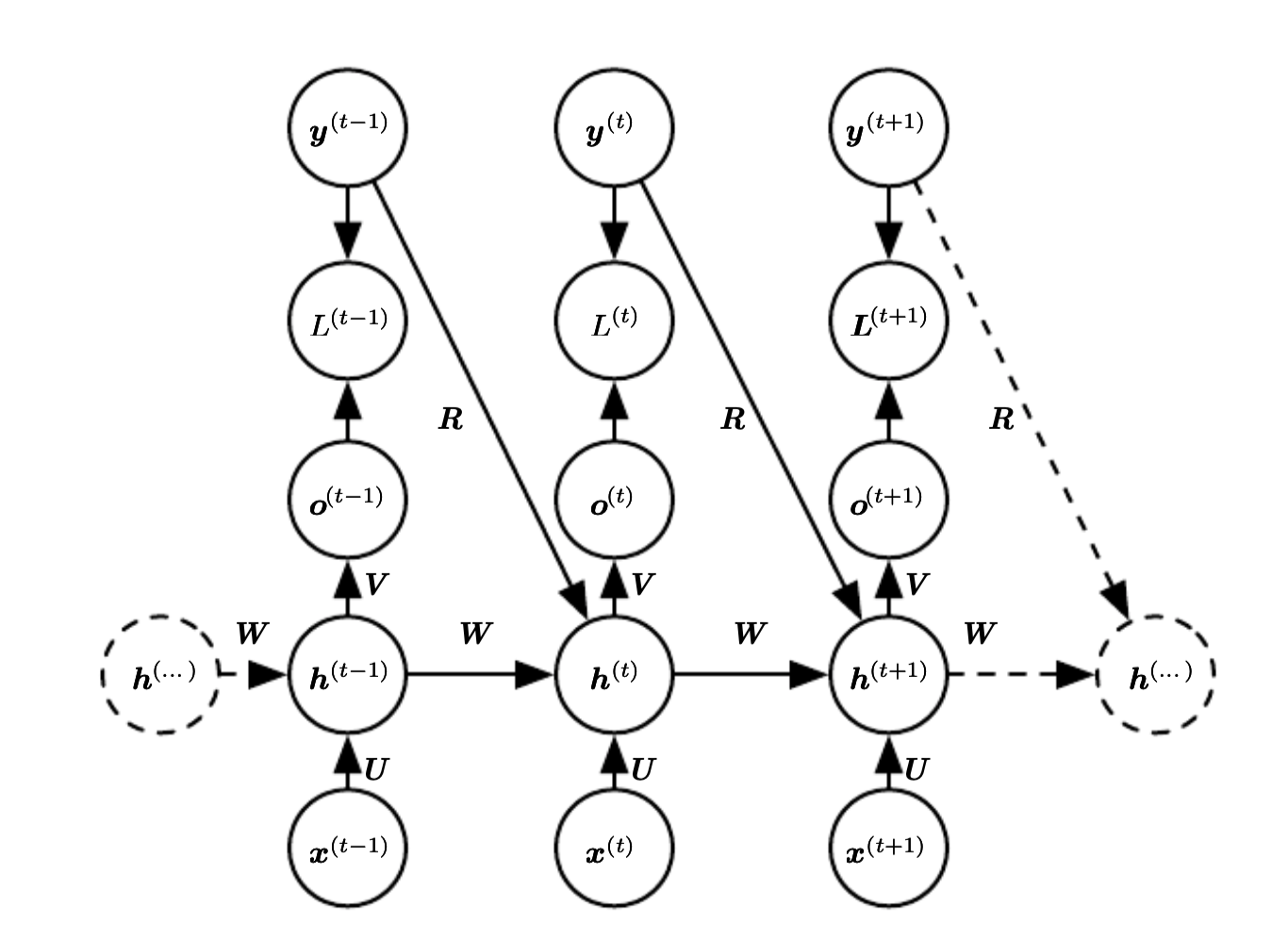
This assumes
\[
\prod_t p(y^{(t)}| x^{(1)}, \cdots, x^{(t)})
\]
We add a connection from t to the output at time t to the hidden units at \(t+1\).
