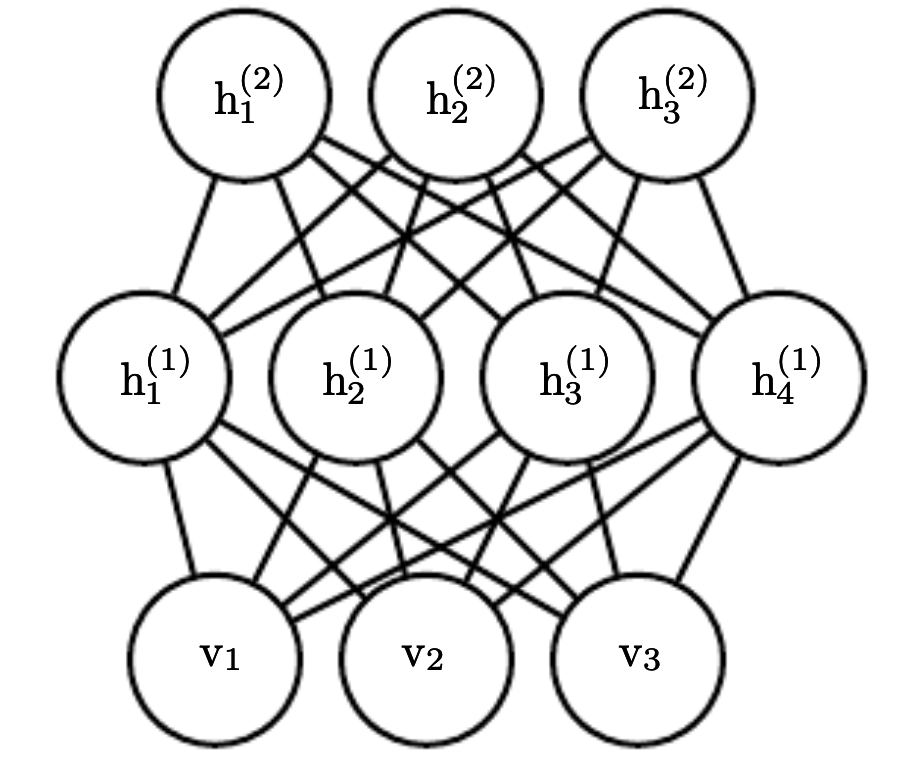
Restricted Boltzman Machine ¶

deep learning model that is also an undirected graphical model.
single layer latent variable model
energy based model with a single visible and hidden unit $$ p(v=v, v=v) = \frac{1}{Z}\exp \{ =E(u,v)\} \\ E(U,V) = -b^Tv - c^Th - v^TWv \\ Z = \sum_u \sum_v \exp\{-E(u,v)\} $$
- $b,c,w$ are unconstrained learned real values
the model is divided int two groups, $h$ (hidden) and $v$ (visible) units and the interactions between them is defined by a matrix $W$

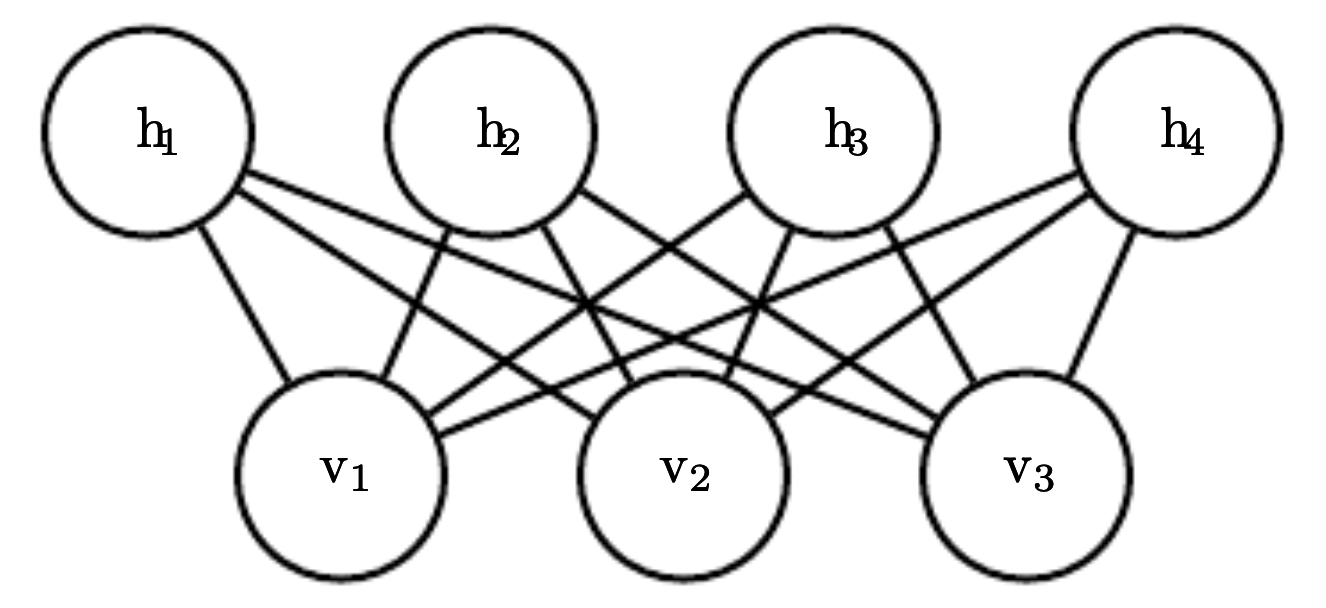
There are not interactions between visible or hidden units (Hense the name restricted)

Conditional distributions¶

\[\begin{split} p(h|v) = \prod_i p(h_i|v) \\ p(v|) = \prod_i p(v_i|h) \end{split}\]

the individual conditionals are: $$ p(h_i = 1|v) = \sigma(v^TW_{:,i} + c_i) \\ p(h_i = 0|v) = 1 - p(h_i = 1|v) $$

we can use block Gibbs sampling alternating between sampling all of the hidden units $h$ and sampling all of the visible units $v$
the derivative of the energy function is $$ \frac{\partial}{\partial w_{i,j}} E[v,h] = -v_ih_j$$