Contents

Importance sampling¶

If we can evaluate \(P(x)\) at any point x up to a multiplicative constant \(P(x) = P^*(x)/Z\), but \(P(x)\) to complex to sample directly. Now we take a simpler distribution \(Q(x)\) which we can draw samples from directly, up to a multiplicative constant \(Q(x) =Q^*(x) / Z_Q\).

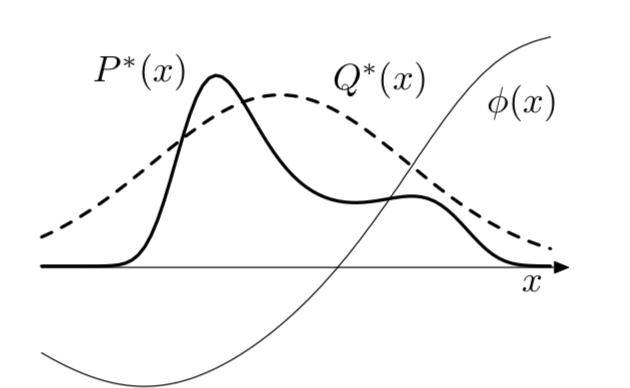
Now some samples x from Q will overestimate P(x) and some samples will under estimate P(x).

Formally we want to compute:

\[\begin{split} E_{x \sim p}[f(x)] = \sum_x f(x)p(x) \\ = \sum_x f(x)\frac{p(x)}{q(x)}q(x) \\ = E_{x \sim q}[f(x)w(x)] \\ = \frac{1}{T} \sum_{i=1}^T f(x^t)w(x^t) \end{split}\]

  • \(w(x) = \frac{p(x)}{q(x)}\) is a weight

  • \(x^t\) are samples drawn form q

Thus we sample from q and we weight them with w, the expectation of this Monte Carlo method is approximation to the original integral.

Choosing the approximation function Q¶

Importance sampling is NOT useful if the importance weights wary substantially. The worst scenario is when the importance ratios are small with high probability, and huge with small probability. This happens if P has wider tails than Q.

Accuracy and efficiency of importance sampling estimates¶

We can analyze the distribution of importance weights to discover possible problems. In general if the largest ratio is too large compared to the average, then the estimates are often poor.

If the variance of the weights is finite we can estimate the effective sample size:

\[S_{eff} = \frac{1}{\sum_{s=1}^S (\tilde{w}(\theta^s))^2} \]

  • \(\tilde{w}(\theta^s) = \frac{w(\theta^s)}{\sum_{s=1}^S w(\theta^s)}\) are the normalized importance weights

If this quantity is small, then there are a few extremely large weights, that influxes the distribution.

Importance re-sampling (SIR sampling-importance re-sampling)¶

Here we want to take importance weights drawn by importance sampling and transform them so we obtain independent samples with equal weights.

We assume that we have S samples \(\{ \theta^1, \cdots, \theta^S \}\) using importance sampling, where each sample \(\theta^i\) has the weights \(w(\theta^i) = \frac{p^*(\theta^s| s)}{g(\theta)}\)

Steps

  1. Sample \(\theta\) from the set of samples \(S\), where the probability of sampling is proportional to \(w(\theta^s)\)

  2. Sample a second value, with the same procedure, but exclude the already sampled value

  3. Repeat without replacement \(k-2\) times.

Remarks¶

Importance sampler should be a distribution that has heavy tails. It is nearly impossible to use in high dimension since it will be dominated by a few huge weights.

Noisy Gaussian process Regerssion Projectile Motion