Convex Functions¶
A function \(f\) is convex if for any two points the following inequality holds:
\(x \ne y\)
\(0 < t < 1\)
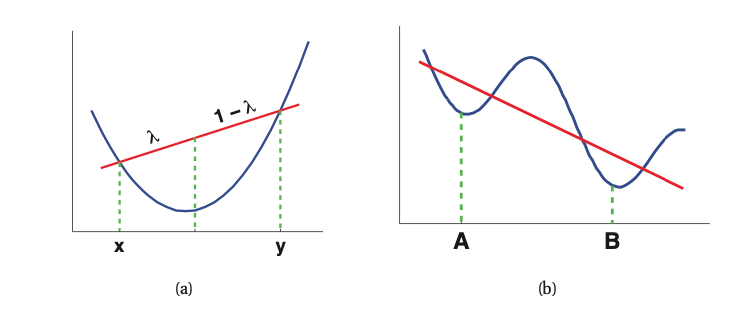
a) is convex, b) is not
Convex sets¶
If a functions \(f\) is defined on a convex set \(S\) and for any \(\theta, \theta' \in S\) and \(0 \le \lambda \le 1\) we have
Strict convexity¶
Same as convex but with strickt inequality.
This means that f is convex and has greater curvature than a linear function.
Strong convexity¶
We say that a function \(f\) is strongly convex when for a paramter \(m > 0\)
If \(g\) is a convex function. This means that f is at least as convex as a quadratic function.
Convex relationship¶
strongly conves => strictly convex => convex
Operations that preserve convexity¶
Nonnegative linear combinations of convex functions
\(f_1a_1 + \cdots + f_na_n\)
\(a_1, \cdots, a_n \ge 0\)
Point wise maximization of a convex function
If \(f_s\) is convex than for any \(s \in S\) point wise maximization \(f(x) = \max_{s\in S}f_s(x)\) yields an convex function.
Partial minimization
If \(g(x,y)\) is convex in x, y and C is convex then \(f(x) = min_{g \in C}g(x,y)\) is convex.
We can minimize over some variables if g is convex and x and y are from an convex Set.
Convexity in higher dimesnions¶
We can expand the notion of convexity to multiple dimensions, than a convex function has to have a bowl shape, that means it will have a unique global minimum \(\theta^*\) corresponding to the bottom of the bowl. This means that the second derivative must be positive everywhere:
A twice differentiable, mutivariable function is convex if its Hessian is positive definite for all \(\theta\).
