Contents

EM For PPCA¶

This is an expectation maximization algorithm for Probabilistic PCA but it works in the limit \(\sigma^2 \rightarrow 0\)

Let \(\tilde{Z}_{L \times N}\) matrix storing the posterior means alog ints columns. And let \(\tilde{X} = X^T\) store the original data along its columns.

\[\begin{split}\text{ E step } \tilde{Z} = (W^TW)^{-1}W^T\tilde{X} \\ \text{M step } W = \tilde{X}\tilde{Z}^T (\tilde{Z} \tilde{Z}^T)^{-1} \end{split}\]

The Physical analogy can be explained as:

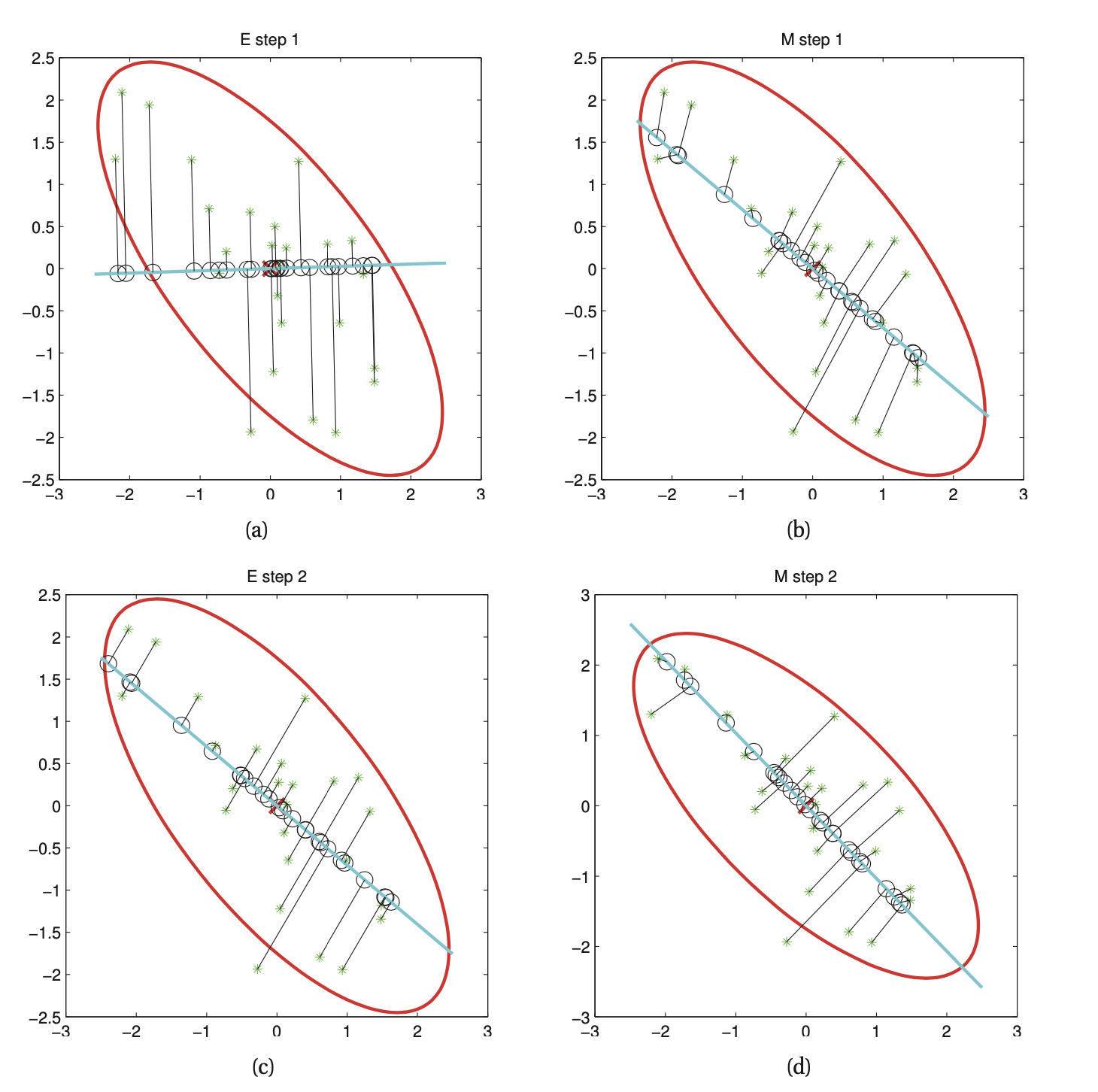
em_pca

Here we can view starts as points an the black line as a string connected to a rod. In the E step, we hold the rod fixed, and let the attachment points slide around so as to minimize the spring energy (which is proportional to the sum of squared residuals). In the M step, we hold the attachment points fixed and let the rod rotate so as to minimize the spring energy.

Advantages of EM for PCA¶

  • Can be faster

  • Can be implemented online fashion

  • Can handle missing points

  • We can modify it to perform variational EM or variational Bayes EM.

Forward vs reverse KL divergence Inequalities