Gaussian Process Regression¶
It is a prior on the regression function defined as:
\(m(x)\) is the mean function
\(\mathcal{k}(x,x')\) is the kernel or covariance function, it requires that
\(m(x) = E[f(x)]\)
\(\mathcal{k}(x, x') = E[(f(x) - m(x))(f(x') - m(k'))^T]\)
\(\mathcal{k}\) is positive definite kernel.
For any finite set of points, this process defines an joint Gaussian:
\(K_{ij} = \mathcal{k}(x_i, x_j)\)
\(\mu = (m(x_1), \cdots, m(x_M))\)
It is common to use a mean function of \(m(x)= 0\), since the GP is flexible enough to model the mean arbitrarly well.
Noise free observations¶
We assume that the obserations are noise free. In this case the Gaussian process has to interpolate the observations.
Noisy observations¶
Here wo do not require that the Gaussian process interpolates the observations (but it has to be close).
Effect of the kernel parameters¶
The predictive performance of GPs depends exclusively on the suitability of the chosen kernel.
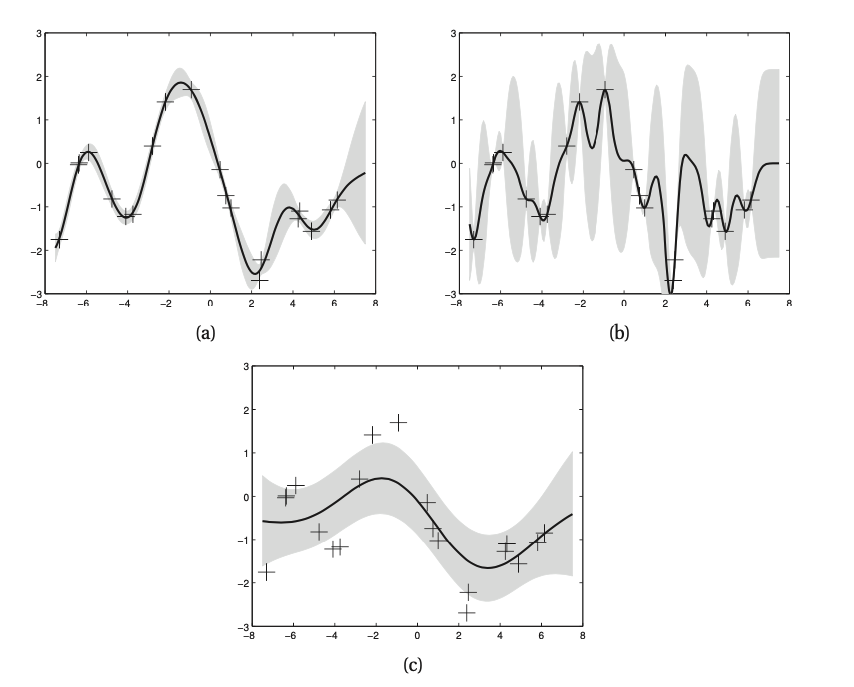
\((l, \sigma_f, \sigma_y)\)
a) Noise free GP with RBF kernel (1,1,0.1)
b) Noise free GP with RBF kernel (0.3, 0.108, 0.00005)
c) Noisy GP with RBF kernel (3.0, 1.15, 0.89)
Semi parametric GP¶
We assume that the mean of the process is a linear model:
\(r(x ) \sim GP(0, k(x,x'))\) models the residuals
Here we combine parametric and nonparametric models (semi-parametric model)
