Conditional independence in Markov Random Fields¶
Two nodes A and B are graph separated if there is no path form A to B. Or we can say that A and B are dependent if they are connected by a path of unobserved variables.
Global Markov property¶
In MRF we define conditional independence relationship via simple graph separation.
For a set of nodes A,B and C we can say that \(x_A \perp_G x_B | x_c\) iff C separates A from B in graph G. This means when we remove all the nodes in C, if there are no paths connecting any node in A to any node in B, then the Ci property holds. This is called the Global Markov property for UGMs.
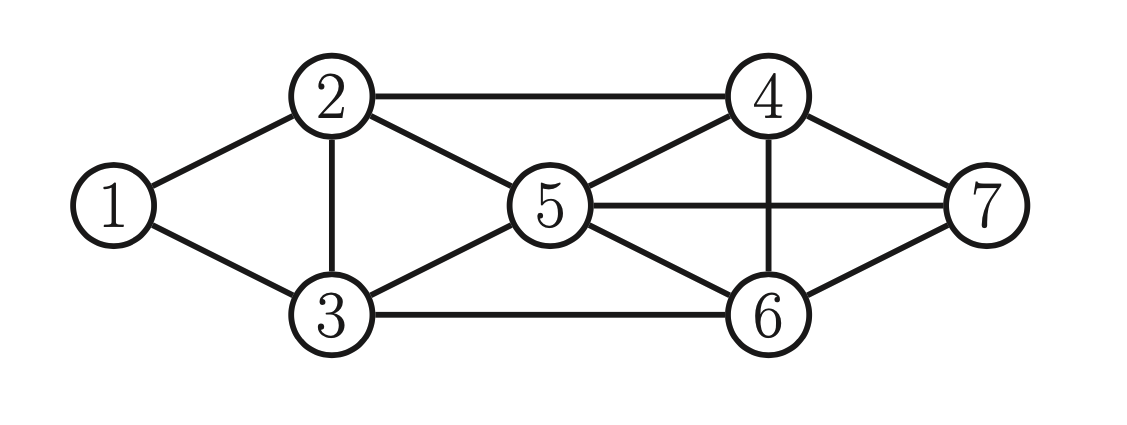We have:
Markov blanket¶
Is the smallest number of nodes that renders a node \(t\) conditionally independent lf all the other nodes in the graph is called \(t\)‘s Markov Blanket, and it is denoted \(mb(t)\). Formally this is:
\(cl(t) \triangleq mb(t) \cup \{t \}\) is the closure of node t
In an UGM a node’s Markov Blanket is its set of immediate neighbors. And it is called undirected local Markov property.
\(mb(5) = \{2,3,4,6,7 \}\)
Pairwise Markov Property¶
From this property we can see that two nodes are conditionally independed given the rest if there is no direct edge between them. More formally:
CI properties in UGM¶
We can summarize different CI properties for:
Pairwise \(1 \perp 7 | rest\)
Local \(1 \perp rest | 2, 3\)
Global \(1,2 \perp 6,7 | 3,4,5\)
There Global Markov implies Local Markov which implies pairwise Markov
Empirically it is easier to asses pairwise conditional independence. Hence we use pairwise CI to construct a graph from which global CI statements can be extracted.
Undirected alternative to d-separation¶
We cannot convert DGM to an UGM just by dropping the orientation of the edges. (To give an example we cannot convert a v-structure \(A \rightarrow B \leftarrow C\) into \(A-B-C\) which states that \(A \perp C | B\) but it muss not hold for the first). To avoid inccorect CI statements, we have to add edges between the “unmarried” parents A and C, and then drop the arrows from the edges, forming a fully connected undirected graph. This process is called normalization:
Example of normalization:
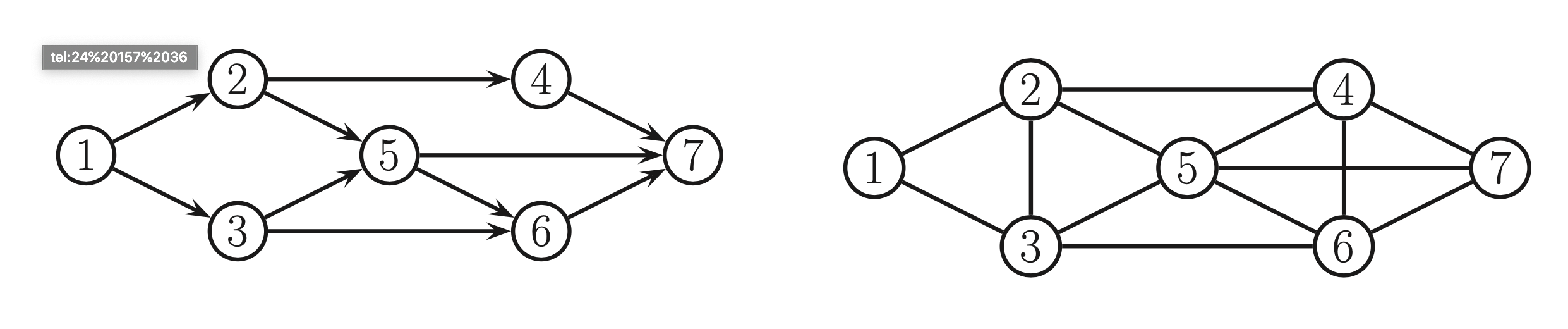
We need to interconnect 2,3 since they have an common child 5, and we interconnect 4,5,6 since they have a common child 7.
Downside of normalization is that we loose some CI information, and therefore we cannot use the normalized UGM to determine the Ci properties of DGM.