Contents

Beta distribution¶

It can be viewed as a generalization of a Uniform distribution over the interval \([0,1]\) where the pdf is non constant.

\[\theta \sim Beta(\alpha, \beta)​\]

Describes the probability of success in a binomial trial, and it is defined in the range \(<0,1>\). This makes it ideal for modeling proportions and percentages.

We recover the uniform distribution on [0,1] by: $\( Unif(0,1) = Beta(1,1) \)$

PDF¶

\[p(\theta|\alpha, \beta) = \frac{1}{B(\alpha,\beta)}\theta^{\alpha - 1}(1-\theta)^{\beta - 1} \]

  • \(0 \le \theta \le 1\)

  • \(\alpha\) - is the shape parameter and it measures the number of successes in an binomial trial \(\alpha -1\)

  • \(\beta\) - is the shape parameter and it measures the number of failures in an binomial trial \(\beta -1\)

  • \(B(\alpha,\beta)\) is the beta function and it is an normalization constant

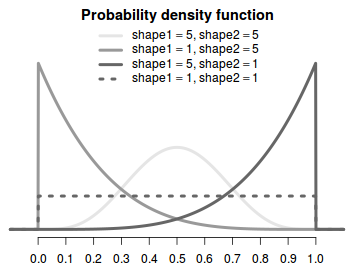
beta_distribution

  1. If \(a < 1\) and \(b < 1\)then the PDF is U shaped and opens upward

  2. If \(a > 1\) and \(b > 1\) then the PDF is U shaped and opens down.

  3. If \(a = b\), then the PDF is symmetric about \(1/2\)

  4. If \(a > b\) then the PDF favors values larger than \(1/2\)

  5. If \(a < b\) then the PDF favors smaller than \(1/2\)

Constructing an beta from its mean and sd¶

\[ \alpha +b = \frac{E[\theta] ( 1 - E[\theta])}{var[\theta] - 1} ​\]

Moments¶

Mean¶

\[E[\theta] = \frac{\alpha}{\alpha + \beta} \]

Variance¶

\[var[\theta]= \frac{\alpha \beta}{ (\alpha + \beta)^2 (\alpha + \beta + 1)}\]

Mode¶

\[ \frac{a - 1}{a+b - 2} \]

Conjugacy¶

It the conjugate prior for:

  • Binomial

  • Bernoulli

  • Geometric

Properties¶

  • \(\alpha = \beta\) the distribution is symmetric about \(\theta\)

  • \(\alpha = \beta = 1\) the distribution is uniform \(\alpha = 0, \beta =1\)

  • Variance is inversely proportional to the total \(\alpha + \beta\) (the total number of trials)

Deep generative models Conditional expectations